
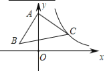
【題目】如圖,在![]() 中,
中,![]() ,頂點
,頂點![]() 在
在![]() 軸上,頂點
軸上,頂點![]() 在反比例函數
在反比例函數![]() 的圖象上,已知點
的圖象上,已知點![]() 的縱坐標是 3,則經過點
的縱坐標是 3,則經過點![]() 的反比例函數的解析式為_____________
的反比例函數的解析式為_____________
【答案】![]()
【解析】
過C作CD⊥y軸于D,過B作BE⊥y軸于E,即可得到△ABE≌△CAD,依據全等三角形的性質以及點C的坐標,即可得到點B的坐標,進而得出經過點B的反比例函數的解析式.
如圖所示,過C作CD⊥y軸于D,過B作BE⊥y軸于E,則∠CDA=∠AEB=90°,
又∵∠BAC=90°,
∴∠BAE+∠CAD=∠ACD+∠CAD=90°,
∴∠BAE=∠ACD,
又∵AB=CA,
∴△ABE≌△CAD(AAS),
又∵頂點C在反比例函數![]()
的圖象上,點C的縱坐標為3,
∴點C的橫坐標為4,
∴CD=4=AE,OD=3,
∴Rt△ACD中,AD= ![]()
= ![]() =2,
=2,
∴BE=AD=2,AO=AD+DO=2+3=5,
∴OE=AO-AE=5-4=1,
∴B(-2,1),
∴經過點B的反比例函數的解析式為![]() .
.
故答案為:![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系 xOy 中,直線 l:![]() 與 x 軸交于點 A(-2,0),與 y 軸交于點 B.雙曲線
與 x 軸交于點 A(-2,0),與 y 軸交于點 B.雙曲線![]() 與直線 l 交于 P,Q 兩點,其中點 P 的縱坐標大于點 Q 的縱坐標.
與直線 l 交于 P,Q 兩點,其中點 P 的縱坐標大于點 Q 的縱坐標.
(1)求點 B 的坐標;
(2)當點 P 的橫坐標為 2 時,求 k 的值;
(3)連接 PO,記△POB 的面積為 S,若![]() ,直接寫出 k 的取值范圍.
,直接寫出 k 的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,設
,設![]() ,
,![]() .
.
(1)如圖1,當點![]() 在
在![]() 內,
內,
①若![]() ,求
,求![]() 的度數;
的度數;
小明同學通過分析已知條件發現:![]() 是頂角為
是頂角為![]() 的等腰三角形,且
的等腰三角形,且![]() ,從而容易聯想到構造一個頂角為
,從而容易聯想到構造一個頂角為![]() 的等腰三角形.于是,他過點
的等腰三角形.于是,他過點![]() 作
作![]() ,且
,且![]() ,連接
,連接![]() ,發現兩個不同的三角形全等:______
,發現兩個不同的三角形全等:______![]() _______再利用全等三角形及等腰三角形的相關知識可求出
_______再利用全等三角形及等腰三角形的相關知識可求出![]() 的度數
的度數
請利用小王同學分析的思路,通過計算求得![]() 的度數為_____;
的度數為_____;
②小王在①的基礎上進一步進行探索,發現![]() 之間存在一種特殊的等量關系,請寫出這個等量關系,并加以證明.
之間存在一種特殊的等量關系,請寫出這個等量關系,并加以證明.
(2)如圖2,點![]() 在
在![]() 外,那么
外,那么![]() 之間的數量關系是否改變?若改變,請直接寫出它們的數量關系;若不變,請說明理由.
之間的數量關系是否改變?若改變,請直接寫出它們的數量關系;若不變,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
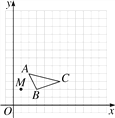
【題目】在13×13的網格圖中,已知△ABC和點M(1,2).
(1)以點M為位似中心,畫出△ABC的位似圖形△A′B′C′,其中△A′B′C′與△ABC的位似比為2;
(2)寫出△A′B′C′的各頂點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
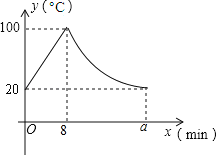
【題目】某小學為每個班級配備了一種可以加熱的飲水機,該飲水機的工作程序是:放滿水后,接通電源,則自動開始加熱,每分鐘水溫上升10℃,待加熱到100℃,飲水機自動停止加熱,水溫開始下降,水溫y(℃)與通電時間x(min)成反比例關系,直至水溫降至室溫,飲水機再次自動加熱,重復上述過程.設某天水溫和室溫為20℃,接通電源后,水溫y(℃)與通電時間x(min)的關系如下圖所示,回答下列問題:
(1)當0≤x≤8時,求y與x之間的函數關系式;
(2)求出圖中a的值;
(3)某天早上7:20,李老師將放滿水后的飲水機電源打開,若他想在8:00上課前能喝到不超過40℃的溫開水,問:他應在什么時間段內接水?
查看答案和解析>>
科目:初中數學 來源: 題型:
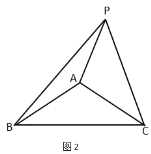
【題目】(1)模型探究:如圖1,![]() 、
、![]() 、
、![]() 分別為
分別為![]() 三邊
三邊![]() 、
、![]() 、
、![]() 上的點,且
上的點,且![]() ,
,![]() 與
與![]() 相似嗎?請說明理由.
相似嗎?請說明理由.

(2)模型應用:![]() 為等邊三角形,其邊長為
為等邊三角形,其邊長為![]() ,
,![]() 為邊
為邊![]() 上一點,
上一點,![]() 為射線
為射線![]() 上一點,將
上一點,將![]() 沿
沿![]() 翻折,使點
翻折,使點![]() 落在射線
落在射線![]() 上的點
上的點![]() 處,且
處,且![]() .
.
①如圖2,當點![]() 在線段
在線段![]() 上時,求
上時,求![]() 的值;
的值;

②如圖3,當點![]() 落在線段
落在線段![]() 的延長線上時,求
的延長線上時,求![]() 與
與![]() 的周長之比.
的周長之比.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=4,AD=3,矩形內部有一動點P滿足S△PAB=![]() S矩形ABCD,則點P到A、B兩點的距離之和PA+PB的最小值為______.
S矩形ABCD,則點P到A、B兩點的距離之和PA+PB的最小值為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC 中,AB=AC,點 M 在 BA 的延長線上,點 N 在 BC 的延長線上,過點 C 作CD∥AB 交∠CAM 的平分線于點 D.
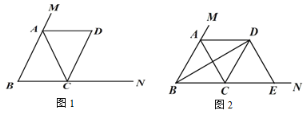
(1)如圖 1,求證:四邊形 ABCD 是平行四邊形;
(2)如圖 2,當∠ABC=60°時,連接 BD,過點 D 作 DE⊥BD,交 BN 于點 E,在不添加任何輔助線的情況下,請直接寫出圖 2 中四個三角形(不包含△CDE),使寫出的每個三角形的面積與△CDE 的面積相等.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com