【題目】將
旋轉一定的角度后得到
，如圖所示，如果
，
．
指出其旋轉中心和旋轉的角度
求
的長度；
與的位置關系如何？說明理由．
【答案】
點
為旋轉中心，對應邊
、
的夾角為旋轉角即
；
；（3）
、
的位置關系為：
．理由見解析.
【解析】
（1）根據旋轉的性質，點D為旋轉中心，對應邊BD、AD的夾角為旋轉角；
（2）根據旋轉的性質可得BD=AD，然后根據勾股定理計算即可；
（3）延長BE交AC于F，根據旋轉可得△BDE和△ADC全等，根據全等三角形對應角相等可得∠DBE=∠DAC，然后求出∠DAC+∠AEF=90°，判斷出BE⊥AC．
（1）由題意可知點D為旋轉中心，對應邊BD、AD的夾角為旋轉角即90°；
（2）根據旋轉的性質可得BD=AD=4cm，CD=2cm，∴AC=
=
=2
cm；
（3）BE、AC的位置關系為：BE⊥AC．理由如下：
延長BE交AC于F．
∵△BDE按順時針方向旋轉一定角度后得到△ADC，∴△BDE≌△ADC，∴∠DBE=∠DAC．
∵∠DBE+∠BED=90°，∴∠DAC+∠AEF=90°，∴∠AFE=180°﹣90°=90°，∴BE⊥AC，∴BE、AC的位置關系為：BE⊥AC．
高中必刷題系列答案科目：初中數學 來源： 題型：
【題目】如圖，將△ABC分別沿AB，AC翻折得到△ABD 和△AEC，線段BD與AE交于點 F，連接BE .
（1）如果∠ABC=16，∠ACB=30°，求∠DAE的度數；
（2）如果BD⊥CE，求∠CAB 的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】隨著近幾年我市私家車日越增多，超速行駛成為引發交通事故的主要原因之一．某中學數學活動小組為開展“文明駕駛、關愛家人、關愛他人”的活動，設計了如下檢測公路上行駛的汽車速度的實驗：先在公路旁邊選取一點
，在筆直的車道
上確定點
，使
和垂直，測得的長等于
米，在上的同側取點
、
，使
，
．
求、之間的路程（保留根號）；
已知本路段對校車限速為
米/秒若測得某校車從到用了
秒，這輛校車是否超速？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
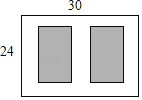
【題目】如圖，某小區有一塊長為30 m，寬為24 m的矩形空地，計劃在其中修建兩塊相同的矩形綠地，它們的面積之和為480 m2，兩塊綠地之間及周邊有寬度相等的人行通道，則人行通道的寬度為________m．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，平面直角坐標系的原點
是正方形
的中心，頂點
，
的坐標分別為
、
，把正方形繞原點逆時針旋轉
得到正方形
，則正方形與正方形重疊部分形成的正八邊形的邊長為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平行四邊形ABCD中，AD＝5cm， AP＝8cm ， AP平分∠DAB，交DC于點P，過點B作BE⊥AD于點E，BE交AP于點F，則tan∠BFP＝ ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某海域有
、
、
三艘船正在捕魚作業，船突然出現故障，向、兩船發出緊急求救信號，此時船位于船的北偏西
方向，距船
海里的海域，船位于船的北偏東
方向，同時又位于船的北偏東
方向．
（1）求
的度數；
船以每小時
海里的速度前去救援，問多長時間能到出事地點．（結果精確到
小時）．（參考數據：
，
）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，把Rt△ABC放在直角坐標系內，其中∠CAB＝90°，BC＝5，點A，B的坐標分別為(1，0)，(4，0)，將△ABC沿x軸向右平移，當點C落在直線y＝2x－6上時，線段BC掃過的面積為________．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
