
【題目】如圖,在平面直角坐標系中,已知拋物線y=![]() x2+
x2+![]() x-2與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,直線l經過A,C兩點,連接BC.
x-2與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,直線l經過A,C兩點,連接BC.
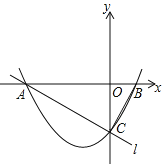
(1)求直線l的解析式;
(2)若直線x=m(m<0)與該拋物線在第三象限內交于點E,與直線l交于點D,連接OD.當OD⊥AC時,求線段DE的長;
(3)取點G(0,-1),連接AG,在第一象限內的拋物線上,是否存在點P,使∠BAP=∠BCO-∠BAG?若存在,求出點P的坐標;若不存在,請說明理由.
【答案】(1)y=![]() x2;(2)
x2;(2)![]() ;(3)P(
;(3)P(![]() ,
,![]() )
)
【解析】
(1)根據題目中的函數解析式可以求得點A和點C的坐標,從而可以求得直線l的函數解析式;
(2)根據題意作出合適的輔助線,利用三角形相似和勾股定理可以解答本題;
(3)根據題意畫出相應的圖形,然后根據銳角三角函數可以求得∠OAC=∠OCB,然后根據題目中的條件和圖形,利用銳角三角函數和勾股定理即可解答本題.
(1)∵拋物線y=![]() x2+
x2+![]() x-2,
x-2,
∴當y=0時,得x1=1,x2=-4,當x=0時,y=-2,
∵拋物線y=![]() x2+
x2+![]() x-2與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,
x-2與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,
∴點A的坐標為(-4,0),點B(1,0),點C(0,-2),
∵直線l經過A,C兩點,設直線l的函數解析式為y=kx+b,
![]() ,得
,得 ,
,
即直線l的函數解析式為y=![]() x2;
x2;
(2)直線ED與x軸交于點F,如圖1所示,
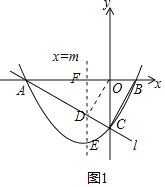
由(1)可得,
AO=4,OC=2,∠AOC=90°,
∴AC=2![]() ,
,
∴OD=![]() ,
,
∵OD⊥AC,OA⊥OC,∠OAD=∠CAO,
∴△AOD∽△ACO,
∴![]() ,
,
即![]() ,得AD=
,得AD=![]() ,
,
∵EF⊥x軸,∠ADC=90°,
∴EF∥OC,
∴△ADF∽△ACO,
∴![]() ,
,
解得,AF=![]() ,DF=
,DF=![]() ,
,
∴OF=4-![]() =
=![]() ,
,
∴m=-![]() ,
,
當m=-![]() 時,y=
時,y=![]() ×(
×(![]() )2+
)2+![]() ×(-
×(-![]() )-2=-
)-2=-![]() ,
,
∴EF=![]() ,
,
∴DE=EF-FD=![]()
![]() =
=![]() ;
;
(3)存在點P,使∠BAP=∠BCO-∠BAG,
理由:作GM⊥AC于點M,作PN⊥x軸于點N,如圖2所示,

∵點A(-4,0),點B(1,0),點C(0,-2),
∴OA=4,OB=1,OC=2,
∴tan∠OAC=![]() ,tan∠OCB=
,tan∠OCB=![]() ,AC=2
,AC=2![]() ,
,
∴∠OAC=∠OCB,
∵∠BAP=∠BCO-∠BAG,∠GAM=∠OAC-∠BAG,
∴∠BAP=∠GAM,
∵點G(0,-1),AC=2![]() ,OA=4,
,OA=4,
∴OG=1,GC=1,
∴AG=![]() ,
,
![]() ,即
,即![]() ,
,
解得,GM=![]() ,
,
∴AM=![]() ,
,
∴tan∠GAM=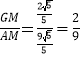 ,
,
∴tan∠PAN=![]() ,
,
設點P的坐標為(n,![]() n2+
n2+![]() n-2),
n-2),
∴AN=4+n,PN=![]() n2+
n2+![]() n-2,
n-2,
∴![]() ,
,
解得,n1=![]() ,n2=-4(舍去),
,n2=-4(舍去),
當n=![]() 時,
時,![]() n2+
n2+![]() n-2=
n-2=![]() ,
,
∴點P的坐標為(![]() ,
,![]() ),
),
即存在點P(![]() ,
,![]() ),使∠BAP=∠BCO-∠BAG.
),使∠BAP=∠BCO-∠BAG.


科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 用適當的統計圖表示某班同學戴眼鏡和不戴眼鏡所占的比例,應繪制折線統計圖
B. 為了解我市某區中小學生每月零花錢的情況,隨機抽取其中800名學生進行調查,這次調查的樣本是800名學生
C. “任意畫出一個平行四邊形,它是中心對稱圖形”是必然事件
D. 若點![]() 在第二象限,則點
在第二象限,則點![]() 在第一象限
在第一象限
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某數學活動小組為測量學校旗桿AB的高度,沿旗桿正前方![]() 米處的點C出發,沿坡角為30°的斜坡CD前進4米到達點D,在點D處安置測角儀,測得旗桿頂部A的仰角為37°,量得儀器的高DE為1.5米.已知A、B、C、D、E在同一平面內,AB⊥BC,AB∥DE.求旗桿AB的高度.(參考數據:sin37°≈
米處的點C出發,沿坡角為30°的斜坡CD前進4米到達點D,在點D處安置測角儀,測得旗桿頂部A的仰角為37°,量得儀器的高DE為1.5米.已知A、B、C、D、E在同一平面內,AB⊥BC,AB∥DE.求旗桿AB的高度.(參考數據:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,計算結果保留根號)
,計算結果保留根號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在某校開展的“好書伴我成長”課外閱讀活動中,為了解八年級學生的課外閱讀情況,隨機抽查部分學生,并對其課外閱讀量進行統計分析,繪制成圖1、圖2兩幅尚不完整的統計圖,請根據圖中信息,解答下列問題:
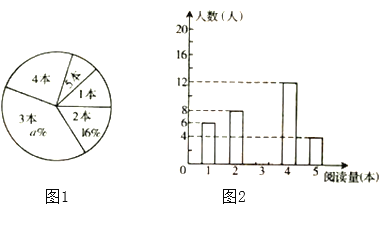
(1)求被抽查的學生人數及課外閱讀量的平均數;
(2)求扇形統計圖中![]() 的值;
的值;
(3)根據樣本數據,估計該校八年級800名學生在本次活動中課外閱讀量多于2本的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
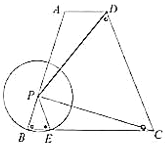
【題目】如圖,將![]() 沿弦
沿弦![]() 折疊,使折疊后的劣弧
折疊,使折疊后的劣弧![]() 恰好經過圓心O,連接
恰好經過圓心O,連接![]() 并延長交
并延長交![]() 于點C,點P是優弧
于點C,點P是優弧![]() 上的動點,連接
上的動點,連接![]() .
.
(1)如圖,用尺規面出折疊后的劣弧![]() 所在圓的圓心
所在圓的圓心![]() ,并求出
,并求出![]() 的度數;
的度數;
(2)如圖,若![]() 是
是![]() 的切線,
的切線,![]() ,求線段
,求線段![]() 的長;
的長;
(3)如圖,連接![]() ,過點B作
,過點B作![]() 的重線,交
的重線,交![]() 的延長線于點D,求證:
的延長線于點D,求證:![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,動點
,動點![]() 在射線
在射線![]() 上,以
上,以![]() 為半徑的
為半徑的![]() 交邊
交邊![]() 于點
于點![]() (點
(點![]() 與點
與點![]() 不重合),聯結
不重合),聯結![]() 、
、![]() ,設
,設![]() ,
,![]() .
.
(1)求證:![]() ;
;
(2)求![]() 關于
關于![]() 的函數解析式,并寫出定義域;
的函數解析式,并寫出定義域;
(3)聯結![]() ,當
,當![]() 時,以
時,以![]() 為圓心半徑為
為圓心半徑為![]() 的
的![]() 與
與![]() 相交,求
相交,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,雙曲線![]() 經過矩形OABC的邊BC的中點E,交AB于點D.設點B的坐標為(m,n).
經過矩形OABC的邊BC的中點E,交AB于點D.設點B的坐標為(m,n).
(1)直接寫出點E的坐標,并求出點D的坐標;(用含m,n的代數式表示)
(2)若梯形ODBC的面積為![]() ,求雙曲線的函數解析式.
,求雙曲線的函數解析式.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校九年級數學小組在課外活動中,研究了同一坐標系中兩個反比例函數![]() 與
與![]()
![]() 在第一象限圖象的性質,經歷了如下探究過程:
在第一象限圖象的性質,經歷了如下探究過程:
操作猜想:
(1)如圖①,當![]() ,
,![]() 時,在
時,在![]() 軸的正方向上取一點
軸的正方向上取一點![]() 作
作![]() 軸的平行線交
軸的平行線交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .當
.當![]() 時,
時,![]() ________,
________,![]() ________,
________,![]() ________;當
________;當![]() 時,
時,![]() ________,
________,![]() ________,
________,![]() ________;當
________;當![]() 時,猜想
時,猜想![]() ________.
________.

數學思考:
(2)在![]() 軸的正方向上任意取點
軸的正方向上任意取點![]() 作
作![]() 軸的平行線,交
軸的平行線,交![]() 于點
于點![]() 、交
、交![]() 于點
于點![]() ,請用含
,請用含![]() 、
、![]() 的式子表示
的式子表示![]() 的值,并利用圖②加以證明.
的值,并利用圖②加以證明.

推廣應用:
(3)如圖③,若![]() ,
,![]() ,在
,在![]() 軸的正方向上分別取點
軸的正方向上分別取點![]() 、
、![]()
![]() 作
作![]() 軸的平行線,交
軸的平行線,交![]() 于點
于點![]() 、
、![]() ,交
,交![]() 于點
于點![]() 、
、![]() ,是否存在四邊形
,是否存在四邊形![]() 是正方形?如果存在,求
是正方形?如果存在,求![]() 的長和點
的長和點![]() 的坐標;如果不存在,請說明理由.
的坐標;如果不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com