
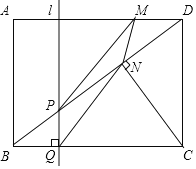
【題目】如圖,在矩形ABCD中,CD=3cm,BC=4cm,連接BD,并過點C作CN⊥BD,垂足為N,直線l垂直BC,分別交BD、BC于點P、Q.直線l從AB出發,以每秒1cm的速度沿BC方向勻速運動到CD為止;點M沿線段DA以每秒1cm的速度由點D向點A勻速運動,到點A為止,直線1與點M同時出發,設運動時間為t秒(t>0).
(1)線段CN= ;
(2)連接PM和QN,當四邊形MPQN為平行四邊形時,求t的值;
(3)在整個運動過程中,當t為何值時△PMN的面積取得最大值,最大值是多少?
【答案】(1)![]() ;(2)t=
;(2)t=![]() ;(3)t=4時,△PMN的面積取得最大值,最大值為
;(3)t=4時,△PMN的面積取得最大值,最大值為![]() .
.
【解析】
(1)由矩形的性質和勾股定理可求BD的長,由三角形的面積公式可求CN的長;
(2)由勾股定理可求DN的長,通過證明△DMN∽△DAB,可得![]() ,可得DM的值,即可求t的值;
,可得DM的值,即可求t的值;
(3)分兩種情況討論,利用三角形面積公式列出△PMN的面積與t的關系式,可求△PMN的面積的最大值.
解:(1)∵四邊形ABCD是矩形
∴BC=AD=4cm,∠BCD=90°=∠A,
∴BD=![]() =5cm,
=5cm,
∵S△BCD=![]() BC
BC![]() CD=
CD=![]() BD
BD![]() CN
CN
∴CN=![]()
故答案為:![]()
(2)在Rt△CDN中,DN=![]() =
=![]()
∵四邊形MPQN為平行四邊形時
∴PQ∥MN,且PQ⊥BC,AD∥BC
∴MN⊥AD
∴MN∥AB
∴△DMN∽△DAB
∴![]()
即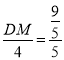
∴DM=![]() cm
cm
∴t=![]()
(3)∵BD=5,DN=![]()
∴BN=![]()
如圖,過點M作MH⊥BD于點H,
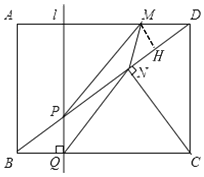
∵sin∠MDH=sin∠BDA=![]()
∴![]()
∴MH=![]() t
t
當0<t<![]()
∵BQ=t,
∴BP=![]() t,
t,
∴PN=BD﹣BP﹣DN=5﹣![]() ﹣
﹣![]() t=
t=![]() ﹣
﹣![]() t
t
∴S△PMN=![]() ×PN×MH=
×PN×MH=![]() ×
×![]() t×(
t×(![]() ﹣
﹣![]() t)=﹣
t)=﹣![]() t2+
t2+![]() t
t
∴當t=![]() s時,S△PMN有最大值,且最大值為
s時,S△PMN有最大值,且最大值為![]() ,
,
當t=![]() s時,點P與點N重合,點P,點N,點M不構成三角形;
s時,點P與點N重合,點P,點N,點M不構成三角形;
當![]() <t≤4時,如圖,
<t≤4時,如圖,

∴PN=BP﹣BN=![]() t﹣
t﹣![]()
∴S△PMN=![]() ×PN×MH=
×PN×MH=![]() ×
×![]() t×(
t×(![]() t﹣
t﹣![]() )=
)=![]() t2﹣
t2﹣![]() t
t
當![]() <t≤4時,S△PMN隨t的增大而增大,
<t≤4時,S△PMN隨t的增大而增大,
∴當t=4時,S△PMN最大值為![]() ,
,
∵![]() >
>![]()
∴綜上所述:t=4時,△PMN的面積取得最大值,最大值為![]() .
.


科目:初中數學 來源: 題型:
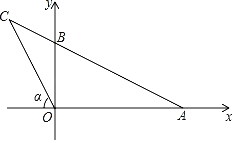
【題目】如圖,在平面直角坐標系中,AB=3![]() ,連結AB并延長至C,連結OC,若滿足OC2=BCAC,tanα=2,則點C的坐標為( )
,連結AB并延長至C,連結OC,若滿足OC2=BCAC,tanα=2,則點C的坐標為( )
A.(﹣2,4)B.(﹣3,6)C.(﹣![]() ,
,![]() )D.(﹣
)D.(﹣![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某數學興趣小組開展了一次課外活動,過程如下:如圖1,正方形ABCD中,AB=6,將三角板放在正方形ABCD上,使三角板的直角頂點與D點重合.三角板的一邊交AB于點P,另一邊交BC的延長線于點Q.
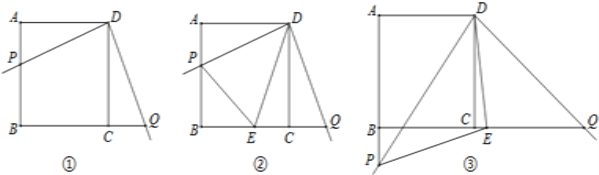
(1)求證:DP=DQ;
(2)如圖2,小明在圖1的基礎上作∠PDQ的平分線DE交BC于點E,連接PE,他發現PE和QE存在一定的數量關系,請猜測他的結論并予以證明;
(3)如圖3,固定三角板直角頂點在D點不動,轉動三角板,使三角板的一邊交AB的延長線于點P,另一邊交BC的延長線于點Q,仍作∠PDQ的平分線DE交BC延長線于點E,連接PE,若AB:AP=3:4,請幫小明算出△DEP的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c(a≠0)與x軸交于點A、B,與y軸分別交于點C,其中點A(﹣1,0),OB=4OA,OC=2OA
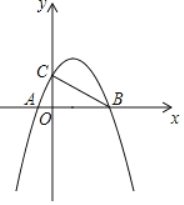
(1)求拋物線的解析式.
(2)點P是線段AB一動點,過P作PD∥AC交BC于D,當△PCD面積最大時,求點P的坐標.
(3)點M是位于線段BC上方的拋物線上一點,當∠ABC恰好等于△BCM中的某個角時,直接寫出點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】據交管部門統計,高速公路超速行駛是引發交通事故的主要原因.我縣某校數學課外小組的幾個同學想嘗試用自己所學的知識檢測車速,渝黔高速公路某路段的限速是:每小時80千米(即最高時速不超過80千米),如圖,他們將觀測點設在到公路l的距離為0.1千米的P處.這時,一輛轎車由綦江向重慶勻速直線駛來,測得此車從A處行駛到B處所用的時間為3秒(注:3秒=![]() 小時),并測得∠APO=59°,∠BPO=45°.試計算AB并判斷此車是否超速?(精確到0.001).(參考數據:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)
小時),并測得∠APO=59°,∠BPO=45°.試計算AB并判斷此車是否超速?(精確到0.001).(參考數據:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)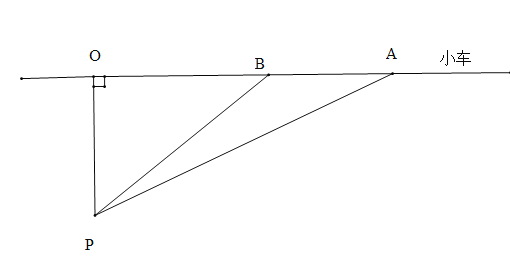
查看答案和解析>>
科目:初中數學 來源: 題型:
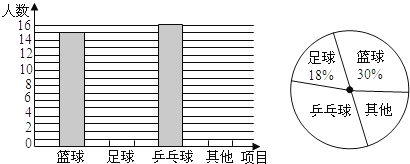
【題目】在大課間活動中,同學們積極參加體育鍛煉,小明就本班同學“我最喜愛的體育項目”進行了一次調查統計,下面是他通過收集數據后,繪制的兩幅不完整的統計圖.請你根據圖中提供的信息,解答以下問題:
(1)該班共有 名學生;
(2)補全條形統計圖;
(3)在扇形統計圖中,“乒乓球”部分所對應的圓心角度數為 ;
(4)學校將舉辦體育節,該班將推選5位同學參加乒乓球活動,有3位男同學(A,B,C)和2位女同學(D,E),現準備從中選取兩名同學組成雙打組合,用樹狀圖或列表法求恰好選出一男一女組成混合雙打組合的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=BC=4,點D在邊BC上,且BD=3CD,DE⊥AB,垂足為點E,聯結CE.
(1)求線段AE的長;
(2)求∠ACE的余切值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】矩形OABC在直角坐標系中的位置如圖所示,A,C兩點的坐標分別為A(6,0),C(0,3),直線![]() 與BC邊相交于點D.
與BC邊相交于點D.

(1)求點D的坐標;
(2)若拋物線![]() 經過D,A兩點,試確定此拋物線的表達式;
經過D,A兩點,試確定此拋物線的表達式;
(3)設(2)中拋物線的對稱軸與直線OD交于點M,點P為對稱軸上一動點,以P、O、M為頂點的三角形與△OCD相似,求出符合條件的P點的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com