
【題目】小蘭和小潭分別用擲A、B兩枚骰子的方法來確定P(x,y)的位置,她們規定:小蘭擲得的點數為x,小譚擲得的點數為y,那么,她們各擲一次所確定的點落在已知直線y=-2x+6上的概率為()
A.![]()
B.![]()
C.![]()
D.![]()
科目:初中數學 來源: 題型:
【題目】已知,直角坐標系中,點E(-4,2),F(-1,-1),以O為位似中心,按比例尺2:1把△EFO縮小,則點E的對應點 ![]() 的坐標為( )
的坐標為( ) 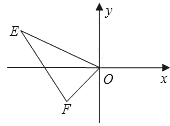
A.(2,-1)或(-2,1)
B.(8,-4)或(-8,4)
C.(2,-1)
D.(8,-4)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C是直線AB,DE之間的一點,∠ACD=90°,下列條件能使得AB∥DE的是( )
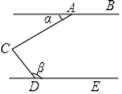
A. ∠α+∠β=180° B. ∠β﹣∠α=90° C. ∠β=3∠α D. ∠α+∠β=90°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某賽季中國職業籃球聯賽第11輪前四名球隊積分榜如下:
隊名 | 比賽場次 | 勝場 | 負場 | 積分 |
遼寧 | 11 | 11 | 0 | 22 |
北京 | 11 | 10 | 1 | 21 |
廣廈 | 11 | 9 | 2 | 20 |
新疆 | 11 | 8 | 3 | 19 |
(1)若一個隊勝m場,則總積分為_____;
(2)某隊的勝場總積分能否等于它的負場總積分,你的觀點是:_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點O為直線AB上一點,過點O作射線OC,使∠BOC=120°.將一直角三角板的直角頂點放在點O處,一邊OM在射線OB上,另一邊ON在直線AB的下方.

(1)將圖1中的三角板繞點O逆時針旋轉至圖2,使一邊OM在∠BOC的內部,且恰好平分∠BOC.問:此時直線ON是否平分∠AOC?請說明理由.
(2)將圖1中的三角板繞點O以每秒10°的速度沿順時針方向旋轉一周,在旋轉的過程中,第t秒時,直線ON恰好平分銳角∠AOC,則 t的值為 秒(直接寫出結果).
(3)將圖1中的三角板繞點O順時針旋轉至圖3,使ON在∠AOC的內部,試探索:在旋轉過程中,∠AOM與∠NOC的差是否發生變化?若不變,請求出這個差值;若變化,請求出差的變化范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
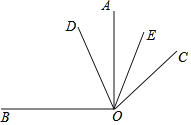
【題目】如圖,已知在同一平面內OA⊥OB,OC是OA繞點O順時針方向旋轉α(α<90°)度得到,OD平分∠BOC,OE平分∠AOC.
(1)若α=60即∠AOC=60°時,求∠BOC,∠DOE.
(2)在α的變化過程中,∠DOE的度數是一個定值嗎?若是定值,請求出這個值;若不是定值,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的袋子里裝有3個黑球和若干白球,它們除顏色外都相同.在不允許將球倒出來數的前提下,小明為估計其中白球數,采用如下辦法:隨機從中摸出一球,記下顏色后放回袋中,充分搖勻后,再隨機摸出一球,記下顏色,…不斷重復上述過程.小明共摸100次,其中20次摸到黑球.根據上述數據,小明估計口袋中白球大約有()
A.10個
B.12 個
C.15 個
D.18個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,∠B的平分線BE與AD交于點E,∠BED的平分線EF與DC交于點F,當點F是CD的中點時,若AB=4,則BC=_________.
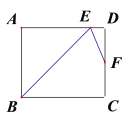
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com