
【題目】如圖,矩形紙片ABCD中,AB=4,BC=8,現把矩形紙片ABCD沿對角線BD折疊,點C與C′重合,求AF的長.
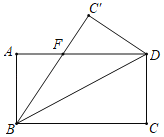
【答案】AF的長為3
【解析】
由矩形的性質可得,AB﹣CD=4,BC=AD=8,∠A=∠ABC=∠C=∠CDA=90°,由折疊得:CD=C′D=4,BC=BC′=8,∠CBD=∠C′BD,進而得到FB=FD,設未知數,將問題轉化到直角三角形ABF中,由勾股定理建立方程求解即可.
∵ABCD是矩形,
∴AB﹣CD=4,BC=AD=8,∠A=∠ABC=∠C=∠CDA=90°,
由折疊得:CD=C′D=4,BC=BC′=8,∠CBD=∠C′BD,
∵∠CBD=∠ADB,
∴∠ADB=∠C′BD,
∴FB=FD,
設AF=x,則FC′=x,FB=FD=8﹣x,
在Rt△ABF中,由勾股定理得,
42+x2=(8﹣x)2,
解得,x=3,即AF=3.
答:AF的長為3.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
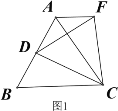
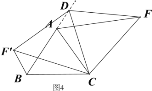
【題目】操作發現:如圖1,D是等邊△ABC邊BA上的一動點(點D與點B不重合),連接DC,以DC為邊在BC上方作等邊△DCF,連接AF,易證AF=BD(不需要證明);
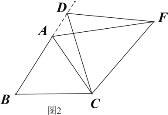
類比猜想:①如圖2,當動點D運動至等邊△ABC邊BA的延長線上時,其它作法與圖1相同,猜想AF與BD在圖1中的結論是否仍然成立。
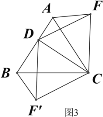
深入探究:②如圖3,當動點D在等邊△ABC邊BA上的一動點(點D與點B不重合),連接DC,以DC為邊在BC上方、下方分別作等邊△DCF和等邊△DCF′,連接AF,BF′你能發現AF,BF′與AB有何數量關系,并證明你發現的結論。
③如圖4,當動點D運動至等邊△ABC邊BA的延長線上時,其它作法與圖3相同,猜想AF,BF′與AB在上題②中的結論是否仍然成立,若不成立,請給出你的結論并證明。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD為正方形,點E為線段AC上一點,連接DE,過點E作EF⊥DE,交射線BC于點F,以DE、EF為鄰邊作矩形DEFG,連接CG.
(1)如圖1,求證:矩形DEFG是正方形;
(2)若AB=2,CE=![]() ,求CG的長度;
,求CG的長度;
(3)當線段DE與正方形ABCD的某條邊的夾角是30°時,直接寫出∠EFC的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
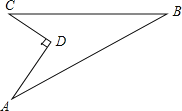
【題目】如圖,某住宅小區在施工過程中留下了一塊空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小區為美化環境,欲在空地上鋪草坪,已知草坪每平方米300元,試問用該草坪鋪滿這塊空地共需花費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有一塊直角三角形紙片,兩直角邊AB=6,BC=8,將△ABC折疊,使AB落在斜邊AC上,折痕為AD,則BD的長為( )

A. 6B. 5C. 4D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠B=32°,將△ABC沿直線m翻折,點B落在點D的位置,則∠1-∠2的度數是( )
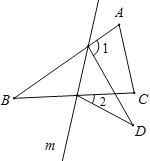
A. 32° B. 64° C. 65° D. 70°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】密碼鎖有三個轉輪,每個轉輪上有十個數字:0,1,2,…9.小黃同學是9月份中旬出生,用生日“月份+日期”設置密碼:9××
小張同學要破解其密碼:
(1)第一個轉輪設置的數字是9,第二個轉輪設置的數字可能是 .
(2)請你幫小張同學列舉出所有可能的密碼,并求密碼數能被3整除的概率;
(3)小張同學是6月份出生,根據(1)(2)的規律,請你推算用小張生日設置的密碼的所有可能個數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com