
【題目】如圖,![]() ,
,![]() 為
為![]() 中點,點
中點,點![]() 在線段
在線段![]() 上(不與點
上(不與點![]() ,
,![]() 重合),將
重合),將![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 后得到扇形
后得到扇形![]() ,
,![]() ,
,![]() 分別切優(yōu)弧
分別切優(yōu)弧![]() 于點
于點![]() ,
,![]() ,且點
,且點![]() ,
,![]() 在
在![]() 異側,連接
異側,連接![]() .
.

(1)求證:![]() ;
;
(2)當![]() 時,求
時,求![]() 的長(結果保留
的長(結果保留![]() );
);
(3)若![]() 的外心在扇形
的外心在扇形![]() 的內部,求
的內部,求![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)![]() ;(3)4<OC<8.
;(3)4<OC<8.
【解析】(1)連接OQ,證明AP,BQ所在兩個三角形全等;(2)在Rt△BOQ中,由OB,BQ的長求出∠BOQ的度數,得到![]() 所對圓心角的度數,再根據弧長公式求解;(3)△APO的外心是OA的中點,
所對圓心角的度數,再根據弧長公式求解;(3)△APO的外心是OA的中點,
試題分析:
試題解析:(1)證明:連接OQ.
∵AP,BQ分別與![]() 相切,∴OP⊥AP,OQ⊥BQ,即∠P=∠Q=90°.
相切,∴OP⊥AP,OQ⊥BQ,即∠P=∠Q=90°.
∵OA=OB,OP=OQ,∴Rt△APO≌Rt△BQO.∴AP=BQ.
(2)∵BQ=![]() ,OB=
,OB=![]() =8,∠Q=90°,∴sin∠BOQ=
=8,∠Q=90°,∴sin∠BOQ=![]() ,∴∠BOQ=60°.
,∴∠BOQ=60°.
∵OQ=8×cos60°=4,∴![]() 的長為
的長為![]() =
=![]() .
.
(3)設點M為Rt△APO的外心,則M為OA的中點,∴OM=4.
當點M在扇形的內部時,OM<OC,∴4<OC<8.
![]()



科目:初中數學 來源: 題型:
【題目】在等邊△ABC中;
(1)如圖1,P,Q是BC邊上兩點,AP=AQ,∠BAP=20°,求∠AQB的度數;
(2)點P,Q是BC邊上的兩個動點(不與點B,C重合),點P在點Q的左側,且AP=AQ,點Q關于直線AC的對稱點為M,連接AM,PM.
①依題意將圖2補全;②小明通過觀察、實驗,提出猜想:在點P,Q運動的過程中,始終有PA=PM,小明把這個猜想與同學們進行交流,通過討論,形成了證明該猜想的幾種想法:
想法1:要證PA=PM,只需證△APM是等邊三角形.
想法2:在BA上取一點N,使得BN=BP,要證PA=PM,只需證△ANP≌△PCM.……
請你參考上面的想法,幫助小明證明PA=PM(一種方法即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某長途汽車客運公司規(guī)定旅客可以免費攜帶一定質量的行李,當行李的質量超過規(guī)定時,需付的行李費y(元)與行李質量x(kg)之間的函數表達式為 ![]() ,這個函數的圖像如圖所示,求:
,這個函數的圖像如圖所示,求:
(1)k和b的值;
(2)旅客最多可免費攜帶行李的質量;
(3)行李費為4~15元時,旅客攜帶行李的質量為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在 Rt△ABC 中,以△ABC 的一邊為邊畫等腰三角形,使得它的第三個頂點在△ABC 的其他邊上,試畫出所有不同的等腰三角形并說明畫圖方法.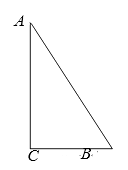
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列調查適合采用抽樣調查的是( )
A.檢查一枚用于發(fā)射衛(wèi)星的運載火箭的各零部件
B.了解全班同學身高狀況
C.檢查一批燈泡的使用壽命
D.奧運會上對參賽運動員進行的尿樣檢查
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com