
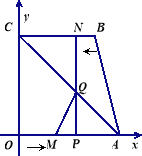
【題目】如圖, 四邊形OABC為直角梯形,A(4,0),B(3,4),C(0,4). 點![]() 從
從![]() 出發以每秒2個單位長度的速度向
出發以每秒2個單位長度的速度向![]() 運動;點
運動;點![]() 從
從![]() 同時出發,以每秒1個單位長度的速度向
同時出發,以每秒1個單位長度的速度向![]() 運動.其中一個動點到達終點時,另一個動點也隨之停止運動.過點
運動.其中一個動點到達終點時,另一個動點也隨之停止運動.過點![]() 作
作![]() 垂直
垂直![]() 軸于點
軸于點![]() ,連結AC交NP于Q,連結MQ.
,連結AC交NP于Q,連結MQ.
【1】點 (填M或N)能到達終點;
【1】求△AQM的面積S與運動時間t的函數關系式,并寫出自變量t的取值范圍,當t為何值時,S的值最大;
【1】是否存在點M,使得△AQM為直角三角形?若存在,求出點M的坐標,若不存在,
![]() 說明理由.
說明理由.
【答案】
【1】點M
【1】經過t秒時,![]() ,
, ![]() ,則
,則![]() ,
,![]()
∵![]() =
=![]() =
=![]() ,∴
,∴![]() ∴
∴![]()
∴![]()
![]()
∴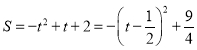 ∵
∵![]() ∴當
∴當![]() 時,S的值最大.
時,S的值最大.
【1】存在。
設經過t秒時,NB=t,OM=2t ,則![]() ,
,![]() ∴
∴![]() =
=![]() =
=![]()
①若![]() ,則
,則![]() 是等腰Rt△
是等腰Rt△![]() 底邊
底邊![]() 上的高,
上的高,
∴![]() 是底邊
是底邊![]() 的中線 ∴
的中線 ∴![]() ,∴
,∴![]() ,∴
,∴![]() , ∴點
, ∴點![]() 的坐標為(1,0)
的坐標為(1,0)
②若![]() ,此時
,此時![]() 與
與![]() 重合,∴
重合,∴![]() ,∴
,∴![]() ,
,
∴![]() ∴點
∴點![]() 的坐標為(2,0)
的坐標為(2,0)
【解析】
【1】由于點M比點N先出發并且點M的速度比點N大,可知點M能到達終點.
【1】經過t秒時可得NB=y,OM-2t.根據∠BCA=∠MAQ=45°推出QN=CN,PQ的值.求出S與t的函數關系式后根據t的值求出S的最大值.
【1】本題分兩種情況討論(若∠AQM=90°,PQ是等腰Rt△MQA底邊MA上的高;
若∠QMA=90°,QM與QP重合)求出t值.


科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC 為等邊三角形,點 D、E 分別在邊 BC、AC 上,且 AE=CD,AD 與 BE相交于點 F.則∠DFE 的度數為_____°;

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示的是麗水市統計局公布的2010~2013年全社會用電量的折線統計圖.

(1)根據統計圖填寫統計表:
2010~2013年麗水市全社會用電量統計表
年份 | 2010 | 2011 | 2012 | 2013 |
全社會用電量 (單位:億KW·h) | 13.33 |
(2)根據麗水市2010年至2013年全社會用電量統計數據,求2011~2013年全社會用電量的年平均增長率(保留到0.01).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=(x﹣1)2+k的圖象與x軸交于點A(﹣1,0),C兩點,與y軸交于點B.
(1)求拋物線解析式及B點坐標;
(2)在拋物線上是否存在點P使S△PAC=![]() S△ABC?若存在,求出P點坐標,若不存在,請說明理由;
S△ABC?若存在,求出P點坐標,若不存在,請說明理由;
(3)在拋物線的對稱軸上是否存在點Q,使△ABQ是等腰三角形,若存在,求出Q點坐標,若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a,b,c為常數,且a≠0)中,x與y的部分對應值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 |
y | 0 | ﹣3 | ﹣4 | ﹣3 |
下列結論:
①ac<0;
②當x>1時,y隨x的增大而增大;
③﹣4是方程ax2+(b﹣4)x+c=0的一個根;
④當﹣1<x<0時,ax2+(b﹣1)x+c+3>0.其中正確結論的個數為( )
A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2-2ax+b經過點C(0,-![]() ),且與x軸交于點A、點B,若tan
),且與x軸交于點A、點B,若tan![]() ACO=
ACO=![]() .
.

(1)求此拋物線的解析式;
(2)若拋物線的頂點為M,點P是線段OB上一動點(不與點B重合),![]() MPQ=45
MPQ=45![]() ,射線PQ與線段BM交于點Q,當△MPQ為等腰三角形時,求點P的坐標.
,射線PQ與線段BM交于點Q,當△MPQ為等腰三角形時,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,某社會實踐活動小組實地測量兩岸互相平行的一段河的寬度,在河的南岸邊點A處,測得河的北岸邊點B在其北偏東45°方向,然后向西走60 m到達點C,測得點B在點C的北偏東60°方向,如圖②.
(1)求∠CBA的度數;
(2)求出這段河的寬(結果精確到1 m,參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73).
≈1.73).

① ②
查看答案和解析>>
科目:初中數學 來源: 題型:
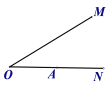
【題目】如圖,兩個30°的角BAC與角MON,頂點A在射線ON上某處,現保持角MON不動,將角BAC繞點A以每秒15°的速度順時針旋轉,邊AB、AC分別與邊OM交于點P、Q,當AC∥OM時,交點Q消失旋轉結束。設運動時間為t秒(t>0).



(1)當t=2秒時,OP:PQ= ;
(2)在運動的過程中,△APQ能否成為等腰三角形?若能,請利用備用圖,直接寫出此時的運動時間;
(3)在(2)中判斷△OAQ的形狀,并選擇其中的一個說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果一個正整數能寫成![]() 的形式(其中a,b均為自然數),則稱之為婆羅摩笈多數,比如7和31均是婆羅摩笈多數,因為7=22+3×12,31=22+3×32。
的形式(其中a,b均為自然數),則稱之為婆羅摩笈多數,比如7和31均是婆羅摩笈多數,因為7=22+3×12,31=22+3×32。
(1)請證明:28和217都是婆羅摩笈多數。
(2)請證明:任何兩個婆羅摩笈多數的乘積依舊是婆羅摩笈多數。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com