
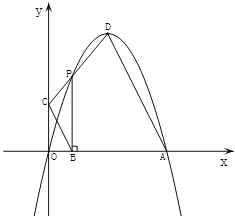
【題目】如圖,拋物線![]() 與
與![]() 軸相交于
軸相交于![]() ,
,![]() 兩點(diǎn),頂點(diǎn)
兩點(diǎn),頂點(diǎn)![]() 在第一象限,點(diǎn)
在第一象限,點(diǎn)![]() 在該拋物線上.
在該拋物線上.
(1)若點(diǎn)![]() 坐標(biāo)為
坐標(biāo)為![]() .
.
①求![]() 與
與![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
②已知兩點(diǎn)![]() ,
,![]() ,當(dāng)拋物線
,當(dāng)拋物線![]() 與線段
與線段![]() 沒有交點(diǎn)時(shí),求
沒有交點(diǎn)時(shí),求![]() 的取值范圍;
的取值范圍;
(2)若![]() 點(diǎn)在該拋物線的曲線段
點(diǎn)在該拋物線的曲線段![]() 上(不與點(diǎn)
上(不與點(diǎn)![]() ,
,![]() 重合),直線
重合),直線![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,過
,過![]() 點(diǎn)作
點(diǎn)作![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,連接
,連接![]() ,
,![]() .求證:
.求證:![]() .
.
【答案】(1)①![]() ;②當(dāng)
;②當(dāng)![]() 或
或![]() 時(shí),該拋物線與線段
時(shí),該拋物線與線段![]() 沒有交點(diǎn).(2)詳見解析.
沒有交點(diǎn).(2)詳見解析.
【解析】
(1)①將點(diǎn)P的坐標(biāo)代入拋物線的解析式即可得;
②當(dāng)拋物線與x軸的另一個(gè)交點(diǎn)在點(diǎn)N的左側(cè)或在點(diǎn)M的右側(cè)時(shí),拋物線與線段MN均無交點(diǎn).方法一:利用拋物線二次項(xiàng)系數(shù)與開口大小的關(guān)系求解;方法二:利用二次函數(shù)圖象的對(duì)稱性及對(duì)稱軸的位置列出不等式求解即可;
(2)如圖(見解析),過![]() 點(diǎn)作
點(diǎn)作![]() 軸于
軸于![]() 點(diǎn),根據(jù)拋物線的解析式可求出點(diǎn)D和A的坐標(biāo),從而可知DH和AH的長,再設(shè)點(diǎn)P的坐標(biāo)為
點(diǎn),根據(jù)拋物線的解析式可求出點(diǎn)D和A的坐標(biāo),從而可知DH和AH的長,再設(shè)點(diǎn)P的坐標(biāo)為![]() ,求出PD所在直線的解析式,從而求得點(diǎn)C的坐標(biāo),也就可以得知OC和OB的長,由此可得
,求出PD所在直線的解析式,從而求得點(diǎn)C的坐標(biāo),也就可以得知OC和OB的長,由此可得![]() ,根據(jù)相似三角形的判定定理與性質(zhì)可得
,根據(jù)相似三角形的判定定理與性質(zhì)可得![]() ,最后根據(jù)平行線的判定定理即可.
,最后根據(jù)平行線的判定定理即可.
(1)①∵拋物線![]() 經(jīng)過
經(jīng)過![]()
![]()
故b與a的函數(shù)關(guān)系式為:![]()
② 由(1)得![]()
方法一,有兩種情況:
(Ⅰ)當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合時(shí)
重合時(shí)
![]() ,解得
,解得![]()
![]() 越大,拋物線開口越小
越大,拋物線開口越小
∴當(dāng)![]() 時(shí),拋物線與線段
時(shí),拋物線與線段![]() 沒有交點(diǎn)
沒有交點(diǎn)
(Ⅱ)當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合時(shí)
重合時(shí)
![]() ,解得
,解得![]()
![]() 越小,拋物線開口越大,且
越小,拋物線開口越大,且![]()
∴當(dāng)![]() 時(shí)拋物線與線段
時(shí)拋物線與線段![]() 沒有交點(diǎn)
沒有交點(diǎn)
綜上所述,當(dāng)![]() 或
或![]() 時(shí),該拋物線與線段
時(shí),該拋物線與線段![]() 沒有交點(diǎn);
沒有交點(diǎn);
方法二,有兩種情況:
(Ⅰ)當(dāng)拋物線與![]() 軸的另一個(gè)交點(diǎn)在
軸的另一個(gè)交點(diǎn)在![]() 點(diǎn)左側(cè)時(shí),拋物線與線段
點(diǎn)左側(cè)時(shí),拋物線與線段![]() 沒有交點(diǎn)
沒有交點(diǎn)
∵拋物線![]() 開口向下,經(jīng)過原點(diǎn)且頂點(diǎn)在第一象限,對(duì)稱軸為
開口向下,經(jīng)過原點(diǎn)且頂點(diǎn)在第一象限,對(duì)稱軸為![]()
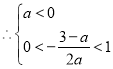
解得![]()
(Ⅱ)當(dāng)拋物線與![]() 軸的另一個(gè)交點(diǎn)在
軸的另一個(gè)交點(diǎn)在![]() 點(diǎn)右側(cè)時(shí),拋物線與線段
點(diǎn)右側(cè)時(shí),拋物線與線段![]() 沒有交點(diǎn)
沒有交點(diǎn)
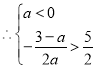
解得![]()
綜上所述,當(dāng)![]() 或
或![]() 時(shí),該拋物線與線段
時(shí),該拋物線與線段![]() 沒有交點(diǎn);
沒有交點(diǎn);
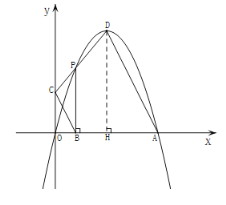
(2)如圖,過![]() 點(diǎn)作
點(diǎn)作![]() 軸于
軸于![]() 點(diǎn)
點(diǎn)
∵拋物線![]() 的頂點(diǎn)
的頂點(diǎn)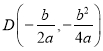
![]()
當(dāng)![]() 時(shí),
時(shí),![]()
∴ 點(diǎn)![]() ,
,![]()
設(shè)直線![]() 為:
為:![]() ,
,![]() ,則
,則![]()
將點(diǎn)P和D的坐標(biāo)代入得: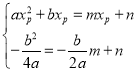 ,解得:
,解得: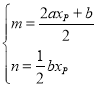
則直線![]() 為:
為:![]()
![]()
![]()
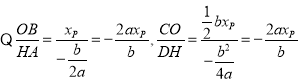
![]()
又![]()
![]()
![]()
![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(10分)如圖,一小球從斜坡O點(diǎn)處拋出,球的拋出路線可以用二次函數(shù)y=﹣x2+4x刻畫,斜坡可以用一次函數(shù)y=![]() x刻畫.
x刻畫.
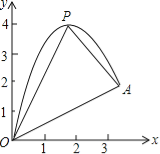
(1)請(qǐng)用配方法求二次函數(shù)圖象的最高點(diǎn)P的坐標(biāo);
(2)小球的落點(diǎn)是A,求點(diǎn)A的坐標(biāo);
(3)連接拋物線的最高點(diǎn)P與點(diǎn)O、A得△POA,求△POA的面積;
(4)在OA上方的拋物線上存在一點(diǎn)M(M與P不重合),△MOA的面積等于△POA的面積.請(qǐng)直接寫出點(diǎn)M的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
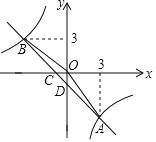
【題目】如圖,一次函數(shù)y=kx+b(k,b為常數(shù),k≠0)的圖象與反比例函數(shù)![]() 的圖象交于A、B兩點(diǎn),且與x軸交于點(diǎn)C,與y軸交于點(diǎn)D,A點(diǎn)的橫坐標(biāo)與B點(diǎn)的縱坐標(biāo)都是3.
的圖象交于A、B兩點(diǎn),且與x軸交于點(diǎn)C,與y軸交于點(diǎn)D,A點(diǎn)的橫坐標(biāo)與B點(diǎn)的縱坐標(biāo)都是3.
(1)求一次函數(shù)的表達(dá)式;
(2)求△AOB的面積;
(3)寫出不等式kx+b>﹣![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB于點(diǎn)H,點(diǎn)F是![]() 上一點(diǎn),連接AF交CD的延長線于點(diǎn)E.
上一點(diǎn),連接AF交CD的延長線于點(diǎn)E.
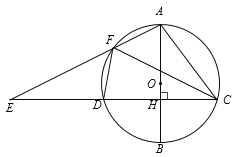
(1)求證:△AFC∽△ACE;
(2)若AC=5,DC=6,當(dāng)點(diǎn)F為![]() 的中點(diǎn)時(shí),求AF的值.
的中點(diǎn)時(shí),求AF的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,拋物線y=ax2﹣4ax﹣![]() (a≠0)交x軸于A、B兩點(diǎn),交y軸于點(diǎn)C,這條拋物線的頂點(diǎn)為D.
(a≠0)交x軸于A、B兩點(diǎn),交y軸于點(diǎn)C,這條拋物線的頂點(diǎn)為D.
(1)求點(diǎn)D的坐標(biāo).
(2)過點(diǎn)C作CE∥x軸交拋物線于點(diǎn)E.當(dāng)CE=2AB時(shí),求點(diǎn)D的坐標(biāo).
(3)這條拋物線與直線y=﹣x相交,其中一個(gè)交點(diǎn)的橫坐標(biāo)為﹣1.過點(diǎn)P(m,0)作x軸的垂線,交這條拋物線于點(diǎn)M,交直線y=﹣x于點(diǎn)N,且點(diǎn)M在點(diǎn)N的下方.當(dāng)線段MN的長度隨m的增大而增大時(shí),求m的取值范圍.
(4)點(diǎn)Q在這條拋物線上運(yùn)動(dòng),若在這條拋物線上只存在兩個(gè)點(diǎn)Q,滿足S△ABQ=3S△ABC,直接寫出a的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
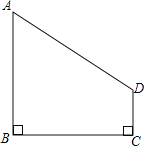
【題目】在四邊形ABCD中,∠B=∠C=90°,若AB=4,BC=4,CD=1,問:在BC上是否存在點(diǎn)P,使得AP⊥PD?若存在,求出BP的長;若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】四張大小、形狀都相同的卡片上分別寫有數(shù)字1,2,3,4,把它們放入不透明的盒子中搖勻.
(1)從中隨機(jī)抽出1張卡片,抽出的卡片上的數(shù)字恰好是偶數(shù)的概率為 .
(2)從中隨機(jī)抽出1張卡片,記錄數(shù)字后放回?fù)u勻,再抽出一張卡片,記錄數(shù)字.用樹狀圖或列表法求兩次抽出的卡片上的數(shù)字恰好是兩個(gè)相鄰整數(shù)的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,O為坐標(biāo)原點(diǎn),點(diǎn)A(3,0),B(3,4).

(1)畫出△AOB繞原點(diǎn)O逆時(shí)針旋轉(zhuǎn)90°得到的△A'OB',并寫出點(diǎn)A',B'的坐標(biāo);
(2)求線段AB在上述旋轉(zhuǎn)過程中掃過的區(qū)域面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在矩形ABCD中,P為CD邊上一點(diǎn)(DP<CP),∠APB=90°.將△ADP沿AP翻折得到△AD′P,PD′的延長線交邊AB于點(diǎn)M,過點(diǎn)B作BN∥MP交DC于點(diǎn)N.
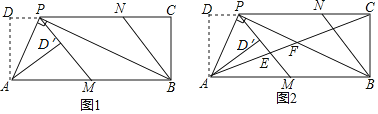
(1)求證:AD2=DPPC;
(2)請(qǐng)判斷四邊形PMBN的形狀,并說明理由;
(3)如圖2,連接AC,分別交PM,PB于點(diǎn)E,F(xiàn).若![]() =
=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com