
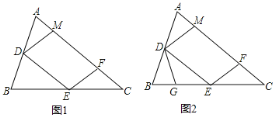
【題目】如圖1,銳角△ABC中,D、E分別是AB、BC的中點,F是AC上的點,且∠AFE=∠A,DM//EF交AC于點M.
(1)求證:DM=DA;
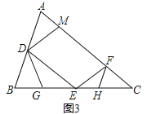
(2)點G在BE上,且∠BDG=∠C,如圖2,
① 求證:△DEG∽△ECF;
② 從線段CE上取一點H,連接FH使∠CFH=∠B,若BG=1,求EH的長.
【答案】(1)見解析 (2)①見解析 ②1
【解析】
(1)根據平行線性質得∠AMD=∠AFE,可證∠AMD=∠A,得DM=DA;
(2)①根據三角形中位線性質得DE∥AC,證∠DEG=∠C,∠GDE=∠FEC,可證△DEG∽△ECF;
②證△BDG∽△BED,得![]() ,BD2=BGBE;證△EFH∽△ECF,得
,BD2=BGBE;證△EFH∽△ECF,得![]() ,EF2=EHEC,又可證四邊形DEFM是平行四邊形,故EF=DM=DA=BD,所以BGBE=EHEC,又BE=EC,故EH=BG.
,EF2=EHEC,又可證四邊形DEFM是平行四邊形,故EF=DM=DA=BD,所以BGBE=EHEC,又BE=EC,故EH=BG.
解:(1)證明:如圖1所示,
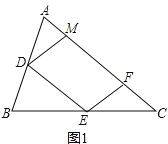
∵DM∥EF,
∴∠AMD=∠AFE,
∵∠AFE=∠A,
∴∠AMD=∠A,
∴DM=DA;
(2)①證明:如圖2所示,
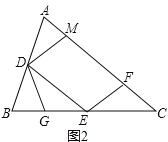
∵D、E分別是AB、BC的中點,
∴DE∥AC,
∴∠BDE=∠A,∠DEG=∠C,
∵∠AFE=∠A,
∴∠BDE=∠AFE,
∴∠BDG+∠GDE=∠C+∠FEC,
∵∠BDG=∠C,
∴∠GDE=∠FEC,
∴△DEG∽△ECF;
②如圖3所示,
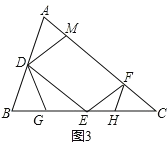
∵∠BDG=∠C=∠DEB,∠B=∠B,
∴△BDG∽△BED,
∴![]() ,
,
∴BD2=BGBE,
∵∠AFE=∠A,∠CFH=∠B,
∴∠C=180°-∠A-∠B=180°-∠AFE-∠CFH=∠EFH,
又∵∠FEH=∠CEF,
∴△EFH∽△ECF,
∴![]() ,
,
∴EF2=EHEC,
∵DE∥AC,DM∥EF,
∴四邊形DEFM是平行四邊形,
∴EF=DM=DA=BD,
∴BGBE=EHEC,
∵BE=EC,
∴EH=BG=1.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:初中數學 來源: 題型:
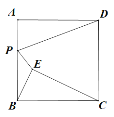
【題目】如圖,已知正方形ABCD的邊長為8,點E是正方形內部一點,連接BE,CE,且∠ABE=∠BCE,點P是AB邊上一動點,連接 PD,PE,則PD+PE長度的最小值為( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知如圖1,四邊形![]() 是正方形,
是正方形,![]() 分別在邊
分別在邊![]() 、
、![]() 上,且
上,且![]() ,我們把這種模型稱為“半角模型”,在解決“半角模型”問題時,旋轉是一種常用的方法.
,我們把這種模型稱為“半角模型”,在解決“半角模型”問題時,旋轉是一種常用的方法.
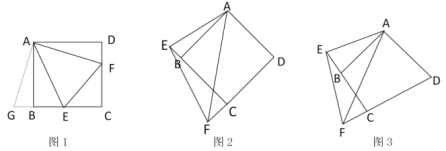
(1)在圖l中,連接![]() ,為了證明結論“
,為了證明結論“![]() ”,小亮將
”,小亮將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 后解答了這個問題,請按小亮的思路寫出證明過程;
后解答了這個問題,請按小亮的思路寫出證明過程;
(2)如圖2,當![]() 繞點
繞點![]() 旋轉到圖2位置時,試探究
旋轉到圖2位置時,試探究![]() 與
與![]() 、
、![]() 之間有怎樣的數量關系?
之間有怎樣的數量關系?
(3)如圖3,如果四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在坐標平面內,△ABC的頂點位置如圖所示.
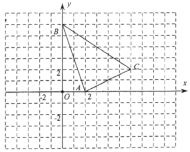
(1)將△ABC作平移交換(x,y)→(x+2,y-3)得到![]() ,畫出
,畫出![]() .
.
(2)以點O為位似中心縮小![]() 得到
得到![]() ,使
,使![]() 與
與![]() 的相似比為1:2,且點A與其對應點
的相似比為1:2,且點A與其對應點![]() 位于點O的兩側,畫出
位于點O的兩側,畫出![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“3.15”植樹節活動后,對栽下的甲、乙、丙、丁四個品種的樹苗進行成活率觀測,以下是根據觀測數據制成的統計圖表的一部分:
栽下的各品種樹苗棵數統計表 | ||||
植樹品種 | 甲種 | 乙種 | 丙種 | 丁種 |
植樹棵數 | 150 | 125 | 125 | |

若經觀測計算得出丙種樹苗的成活率為89.6%,請你根據以上信息解答下列問題:
(1)這次栽下的四個品種的樹苗共 棵,乙品種樹苗 棵;
(2)圖1中,甲 %、乙 %,并將圖2補充完整;
(3)求這次植樹活動的樹苗成活率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在同一直線上有A、B兩地,甲車從A地送貨到B地,同時乙車從B地前往A地,兩車皆勻速行駛.途中某一時刻,甲車發現有貨物落在A、B之間的某處C地,于是立刻掉頭并以自己原來速度的兩倍勻速返回,取到貨物后,再以最初的速度繼續勻速向B地行駛.兩車之間的距離y(千米)與甲車行駛的時間x(小時)之間的函數關系如圖所示(途中掉頭、取貨物耽誤時間忽略不計),當乙車到達A地時,甲車到A地的距離為_____千米.
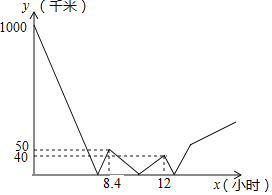
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=﹣![]() x+c與x軸交于點A(3,0),與y軸交于點B,拋物線y=﹣
x+c與x軸交于點A(3,0),與y軸交于點B,拋物線y=﹣![]() x2+bx+c經過點A,B.
x2+bx+c經過點A,B.
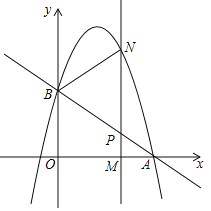
(1)求點B的坐標和拋物線的解析式;
(2)M(m,0)為線段OA上一個動點,過點M垂直于x軸的直線與直線AB和拋物線分別交于點P、N.
①試用含m的代數式表示線段PN的長;
②求線段PN的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ACB中,∠ACB=90°,AC=2BC=4,點P為AB邊中點,點E為AC邊上不與端點重合的一動點,將△ADP沿著直線PD折疊得△PDE,若DE⊥AB,則AD的長度為_____ .

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com