
【題目】已知,在長方形![]() 中,
中,![]() ,
,![]() ,點
,點![]() ,
,![]() 分別是邊
分別是邊![]() ,
,![]() 上的點,連接
上的點,連接![]() ,
,![]() ,
,![]() .
.

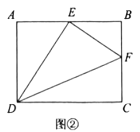
(1)如圖①,當![]() 時,試說明
時,試說明![]() 是直角三角形;
是直角三角形;
(2)如圖②,若點![]() 是邊
是邊![]() 的中點,
的中點,![]() 平分
平分![]() ,求
,求![]() 的長.
的長.
【答案】(1)見解析;(2)![]() .
.
【解析】
(1)根據![]() ,
,![]() ,
,![]() 可求出AE、BF的長,利用勾股定理可分別求出DE、EF、DF的長,根據勾股定理逆定理即可得答案;
可求出AE、BF的長,利用勾股定理可分別求出DE、EF、DF的長,根據勾股定理逆定理即可得答案;
(2)如圖,作![]() 于
于![]() ,利用AAS可證明
,利用AAS可證明![]() ,可得
,可得![]() ,
,![]() ,根據點E為AB中點可得EB=4,即可證明EH=EB,利用HL可證明
,根據點E為AB中點可得EB=4,即可證明EH=EB,利用HL可證明![]() ,可得BF=HF,設
,可得BF=HF,設![]() ,可得
,可得![]() ,DF=6+x,在
,DF=6+x,在![]() 中,利用勾股定理列方程求出x的值即可得答案.
中,利用勾股定理列方程求出x的值即可得答案.
(1)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,BF=4,
,BF=4,
∵四邊形![]() 是長方形,
是長方形,
∴![]() .
.
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() 是直角三角形,且
是直角三角形,且![]() .
.
(2)如圖,作![]() 于
于![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
在![]() 與
與![]() 中,
中,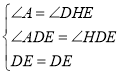 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵點E為AB中點,
∴BE=AE=4,
∴![]()
在![]() 與
與![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
設![]() ,則
,則![]() ,
,![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】已知一次函數y=kx+b的圖象過A(1,1)和B(2,﹣1)
(1)求一次函數y=kx+b的表達式;
(2)求直線y=kx+b與坐標軸圍成的三角形的面積;
(3)將一次函數y=kx+b的圖象沿y軸向下平移3個單位,則平移后的函數表達式為 ,再向右平移1個單位,則平移后的函數表達式為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+2ax+3a2+3(其中x是自變量),當x≥2時,y隨x的增大而增大,且2≤x≤1時,y的最大值為9,則a的值為
A. 1或2 B. ![]() 或
或![]()
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,為了測量河對岸l1上兩棵古樹A、B之間的距離,某數學興趣小組在河這邊沿著與AB平行的直線l2上取C、D兩點,測得∠ACB=15°,∠ACD=45°,若l1、l2之間的距離為50m,則A、B之間的距離為( )
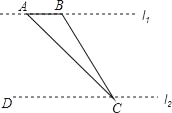
A. 50m B. 25m C. (50﹣![]() )m D. (50﹣25
)m D. (50﹣25![]() )m
)m
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,∠ABC=∠BCD=90°,點E為BC的中點,AE⊥DE.
(1)求證:△ABE∽△ECD;
(2)求證:AE2=AB·AD;
(3)若AB=1,CD=4,求線段AD,DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某村計劃建造如圖所示的矩形蔬菜溫室,要求長與寬的比為2:1.在溫室內,沿前側內墻保留3m寬的空地,其它三側內墻各保留1m寬的通道.當矩形溫室的長與寬各為多少時,蔬菜種植區域的面積是288m2?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com