
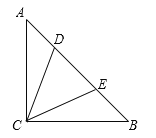
【題目】如圖,在![]() 中,
中,![]() ,以
,以![]() 為直徑的
為直徑的![]() 交邊
交邊![]() 于點
于點![]() (點
(點![]() 不與點
不與點![]() 重合),交邊
重合),交邊![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() ,垂足為
,垂足為![]() .
.
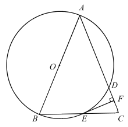
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)若![]() ,
,![]() .
.
①求![]() 的半徑;
的半徑;
②連接![]() 交
交![]() 于點
于點![]() ,則
,則![]() _____.
_____.
【答案】(1)見解析;(2)①4;②![]()
【解析】
(1)連接OE.根據(jù)等腰三角形的性質(zhì)得到∠OEB=∠C,根據(jù)平行線的性質(zhì)得到∠OEF+∠AFE=180°.根據(jù)切線的判定定理即可得到結(jié)論;
(2)①連接BD,AE,根據(jù)圓周角定理得到∠ADB=90°,∠AEB=90°,求得AE⊥BC.根據(jù)勾股定理即可得到結(jié)論;
②根據(jù)勾股定理得到![]() ,CD=1,根據(jù)相似三角形的性質(zhì)得到
,CD=1,根據(jù)相似三角形的性質(zhì)得到![]() ,根據(jù)勾股定理即可得到結(jié)論.
,根據(jù)勾股定理即可得到結(jié)論.
(1)連接![]() .
.
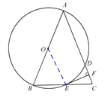
∵在![]() 中,
中,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() 于點
于點![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∵![]() 于點
于點![]() ,
,![]() 是
是![]() 的半徑,
的半徑,
∴![]() 是
是![]() 的切線.
的切線.
(2)①連接![]() .
.
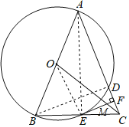
∵![]() 是
是![]() 的直徑,
的直徑,
∴![]() ,
,![]() .
.
∴![]() .
.
∵在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∴AB2-AD2=BC2-CD2.
設(shè)![]() ,則
,則![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
②:∵AD=7,AB=AC=8,
∴![]() ,CD=1,
,CD=1,
∵BE=CE=2,EF∥BD,
∴![]() ,
,![]() ,
,
∵AB=AC,AE⊥BC,
∴∠BAE=∠CAE,
∴![]() ,
,
∴OE⊥BD,
∴OE⊥EF,
∴OE∥CF,
∴△CFM∽△OEM,
∴![]() ,
,
∴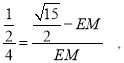
∴![]() ,
,
∴![]() .
.
故答案為:![]() .
.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB = 90°,![]() ,點D、E分別在邊AB上,且AD = 2,∠DCE = 45°,那么DE =___________.
,點D、E分別在邊AB上,且AD = 2,∠DCE = 45°,那么DE =___________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲乙兩人在相同條件下完成了10次射擊訓(xùn)練,兩人的成績?nèi)鐖D所示。

根據(jù)以上信息,整理分析數(shù)據(jù)如下:
平均成績/環(huán) | 中位數(shù)/環(huán) | 方差/環(huán) | |
甲 | ______ | 7 | 1.2 |
乙 | 7 | ______ | ______ |
(1)完成表格;
(2)根據(jù)訓(xùn)練成績,你認(rèn)為選派哪一名隊員參賽更好?為什么?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】受“新冠”疫情的影響,某銷售商在網(wǎng)上銷售![]() 、
、![]() 兩種型號的“手寫板”,獲利頗豐.已知
兩種型號的“手寫板”,獲利頗豐.已知![]() 型,
型,![]() 型手寫板進(jìn)價、售價和每日銷量如表格所示:
型手寫板進(jìn)價、售價和每日銷量如表格所示:
進(jìn)價(元/個) | 售價(元/個) | 銷量(個/日) | |
|
|
|
|
|
|
|
|
根據(jù)市場行情,該銷售商對![]() 型手寫板降價銷售,同時對
型手寫板降價銷售,同時對![]() 型手寫板提高售價,此時發(fā)現(xiàn)
型手寫板提高售價,此時發(fā)現(xiàn)![]() 型手寫板每降低
型手寫板每降低![]() 元就可多賣
元就可多賣![]() 個,
個,![]() 型手寫板每提高
型手寫板每提高![]() 元就少賣
元就少賣![]() 個,要保持每天銷售總量不變,設(shè)其中
個,要保持每天銷售總量不變,設(shè)其中![]() 型手寫板每天多銷售
型手寫板每天多銷售![]() 個,每天總獲利的利潤為
個,每天總獲利的利潤為![]() 元
元
(1)求![]() 與
與![]() 之間的函數(shù)關(guān)系式并寫出
之間的函數(shù)關(guān)系式并寫出![]() 的取值范圍;
的取值范圍;
(2)要使每天的利潤不低于![]() 元,直接寫出
元,直接寫出![]() 的取值范圍;
的取值范圍;
(3)該銷售商決定每銷售一個![]() 型手寫板,就捐
型手寫板,就捐![]() 元給
元給![]() 因“新冠疫情”影響的困難家庭,當(dāng)
因“新冠疫情”影響的困難家庭,當(dāng)![]() 時,每天的最大利潤為
時,每天的最大利潤為![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在一個不透明的口袋里裝有分別標(biāo)有數(shù)字-3、-1、0、2的四個小球,除數(shù)字不同外,小球沒有任何區(qū)別,每次試驗先攪拌均勻.
(1)從中任取一球,將球上的數(shù)字記為a,則關(guān)于x的元二次方程x2-2x-a+1=0有實數(shù)根的概率______;
(2)從中任取一球,將球上的數(shù)字作為點的橫坐標(biāo),記為x(不放回);再任取一球,將球上的數(shù)字作為點的縱坐標(biāo),記為y,試用畫樹狀圖(或列表法)表示出點(x,y)所有可能出現(xiàn)的結(jié)果,并求點(x,y)落在第三象限內(nèi)的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為實現(xiàn)區(qū)域教育均衡發(fā)展,我市計劃對某縣A、B兩類薄弱學(xué)校全部進(jìn)行改造.根據(jù)預(yù)算,共需資金1555萬元改造一所A類學(xué)校和兩所B類學(xué)校共需資金230萬元;改造兩所A類學(xué)校和一所B類學(xué)校共需資金205萬元
(1)改造一所A類學(xué)校和一所B類學(xué)校所需的資金分別是多少萬元?
(2)根據(jù)我市教育局規(guī)劃計劃今年對該縣A、B兩類學(xué)校進(jìn)行改造,要求改造的A類學(xué)校是B類學(xué)校的2倍多2所,在計劃投入資金不超過1555萬元的條件下,至多能改造多少所A類學(xué)校?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】定義:點P是△ABC內(nèi)部或邊上的點(頂點除外),在△PAB,△PBC,△PCA中,若至少有一個三角形與△ABC相似,則稱點P是△ABC的自相似點.
例如:如圖1,點P在△ABC的內(nèi)部,∠PBC=∠A,∠PCB=∠ABC,則△BCP∽△ABC,故點P為△ABC的自相似點.
請你運用所學(xué)知識,結(jié)合上述材料,解決下列問題:
在平面直角坐標(biāo)系中,點M是曲線C:![]()
![]() 上的任意一點,點N是x軸正半軸上的任意一點.
上的任意一點,點N是x軸正半軸上的任意一點.
(1) 如圖2,點P是OM上一點,∠ONP=∠M, 試說明點P是△MON的自相似點; 當(dāng)點M的坐標(biāo)是![]() ,點N的坐標(biāo)是
,點N的坐標(biāo)是![]() 時,求點P 的坐標(biāo);
時,求點P 的坐標(biāo);
(2) 如圖3,當(dāng)點M的坐標(biāo)是![]() ,點N的坐標(biāo)是
,點N的坐標(biāo)是![]() 時,求△MON的自相似點的坐標(biāo);
時,求△MON的自相似點的坐標(biāo);
(3) 是否存在點M和點N,使△MON無自相似點,?若存在,請直接寫出這兩點的坐標(biāo);若不存在,請說明理由.



查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com