【題目】如圖，△ABC中，∠A=100°，BI、CI分別平分∠ABC，∠ACB，則∠BIC=________，若BM、CM分別平分∠ABC，∠ACB的外角平分線，則∠M=__________．
【答案】 140° 40°
【解析】∵∠A=100°，
∵∠ABC+∠ACB=180°100°=80°，
∵BI、CI分別平分∠ABC，∠ACB，
∴∠IBC=
∠ABC，∠ICB=
∠ACB，
∴∠IBC+∠ICB=
∠ABC+
∠ACB=
(∠ABC+∠ACB)= 
×80°=40°，
∴∠BIC=180°(∠IBC+∠ICB)=180°40°=140°，
∵∠ABC+∠ACB=80°，
∴∠DBC+∠ECB=180°∠ABC+180°∠ACB=360°(∠ABC+∠ACB)=360°80°=280°，
∵BM、CM分別平分∠ABC，∠ACB的外角平分線，
∴∠1=
∠DBC，∠2=
∠ECB，
∴∠1+∠2=
×280°=140°，
∴∠M=180°∠1∠2=40°.
故答案為：40°.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】某校為了了解學生家長對孩子用手機的態度問題，隨機抽取了100名家長進行問卷調查，每位學生家長只有一份問卷，且每份問卷僅表明一種態度（這100名家長的問卷真實有效），將這100份問卷進行回收整理后，繪制了如下兩幅不完整的統計圖．
（1）“從來不管”的問卷有 份，在扇形圖中“嚴加干涉”的問卷對應的圓心角為 ．
（2）請把條形圖補充完整．
（3）若該校共有學生2000名，請估計該校對手機問題“嚴加干涉”的家長有多少人．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，分別在三角形、四邊形、五邊形的廣場各角修建半徑為R的扇形草坪(圖中陰影部分)．
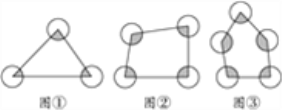
(1)圖①中草坪的面積為__________；
(2)圖②中草坪的面積為__________；
(3)圖③中草坪的面積為__________；
(4)如果多邊形的邊數為n，其余條件不變，那么，你認為草坪的面積為__________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一個不透明的袋子中裝有紅、白兩種顏色的小球，這些球除顏色外都相同，其中紅球有1個，若從中隨機摸出一個球，這個球是白球的概率為
．
（1）求袋子中白球的個數；（請通過列式或列方程解答）
（2）隨機摸出一個球后，放回并攪勻，再隨機摸出一個球，求兩次都摸到相同顏色的小球的概率．（請結合樹狀圖或列表解答）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】概念學習
規定：求若干個相同的有理數（均不等于0）的除法運算叫做除方，如2÷2÷2，
（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等．類比有理數的乘方，我們把2÷2÷2記作2③，讀作“2的圈3次方”，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）記作（﹣3）④，讀作“﹣3的圈4次方”，一般地，把
（a≠0）記作a，讀作“a的圈n次方”．
初步探究
（1）直接寫出計算結果：2③=________， 
⑤=________；
（2）關于除方，下列說法錯誤的是________
A．任何非零數的圈2次方都等于1； B．對于任何正整數n，1
=1； C.3④=4③ D．負數的圈奇數次方結果是負數，負數的圈偶數次方結果是正數．
深入思考
我們知道，有理數的減法運算可以轉化為加法運算，除法運算可以轉化為乘法運算，有理數的除方運算如何轉化為乘方運算呢？
（1）試一試：仿照上面的算式，將下列運算結果直接寫成冪的形式．（﹣3）④=________；5⑥=________； 
⑩=________．
（2）想一想：將一個非零有理數a的圈n次方寫成冪的形式等于________；
（3）算一算： 
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com