
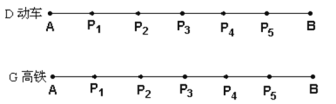
【題目】以下是兩張不同類型火車的車票(“![]() 次”表示動車,“
次”表示動車,“![]() 次”表示高鐵):
次”表示高鐵):

⑴根據車票中的信息填空:該列動車和高鐵是__ _向而行(填“相”或“同”).
⑵知該列動車和高鐵的平均速度分別為![]() 、
、![]() ,兩列火車的長度不計.
,兩列火車的長度不計.
通過測算,如果兩列火車直達終點(即中途都不停靠任何站點),高鐵比動車將早到![]() ,求
,求![]() 、
、![]() 兩地之間的距離.
兩地之間的距離.
②在①中測算的數據基礎上,已知![]() 、
、![]() 兩地途中依次設有
兩地途中依次設有![]() 個站點
個站點![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,且
,且![]() ,動車每個站點都停靠,高鐵只停靠
,動車每個站點都停靠,高鐵只停靠![]() 、
、![]() 兩個站點,兩列火車在每個停靠站點都停留
兩個站點,兩列火車在每個停靠站點都停留![]() .求該列高鐵追上動車的時刻.
.求該列高鐵追上動車的時刻.
【答案】(1)同;(2)①1200km;② 8點55分.
【解析】
(1)根據列車示意圖可知是同向;
(2)①設![]() 之間的距離為
之間的距離為![]() ,根據速度與時間的關系可列方程進行求解;
,根據速度與時間的關系可列方程進行求解;
②根據題意寫出到達每個站點的時間,可知高鐵在![]() 站、
站、![]() 站之間追上并超過動車,設設高鐵經過
站之間追上并超過動車,設設高鐵經過![]() 小時之后追上動車,根據題意列出方程即可進行求解.
小時之后追上動車,根據題意列出方程即可進行求解.
(![]() )根據列車示意圖可知是同向;
)根據列車示意圖可知是同向;
(![]() )設
)設![]() 之間的距離為
之間的距離為![]() ,則可列方程:
,則可列方程:
![]() ,
,
解得![]() .
.
所以![]() 之間的距離為
之間的距離為![]() .
.
(![]() )
)![]() 、
、![]() 兩地之間依次設有
兩地之間依次設有![]() 個距離相同的站點,可知每個相鄰站點距離為
個距離相同的站點,可知每個相鄰站點距離為![]() ,
,
已知動車和高鐵速度,可知高鐵到每一站所花時間為![]() 分鐘,動車到每一站所花時間為60分鐘.
分鐘,動車到每一站所花時間為60分鐘.
根據題意,可知動車和高鐵到每一站的時刻如圖所示:
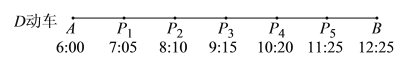
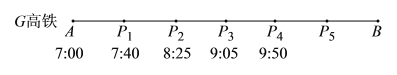
可知高鐵在![]() 站、
站、![]() 站之間追上并超過動車,
站之間追上并超過動車,
設高鐵經過![]() 小時之后追上動車,
小時之后追上動車,
由題意可列方程:![]() ,
,
解得:![]()
∴高鐵在![]() 出發,經過
出發,經過![]() 小時后,追上動車.
小時后,追上動車.
答:該列高鐵追上動車的時刻為8點55分.


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案 新思維寒假作業系列答案
新思維寒假作業系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,一次函數的圖象經過點A(2,3)與點B(0,5).
(1)求此一次函數的表達式;
(2)若點P為此一次函數圖象上一點,且△POB的面積為10,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了創建書香校園,今年又購進一批圖書,經了解,科普書的單價比文學書的單價多4元,用1200元購進的科普書與用800元購進的文學書本數相等.
(1)今年購進的文學書和科普書的單價各是多少元?
(2)該校購買這兩種書共180本,總費用不超過2000元,且購買文學書的數量不多于42本,應選擇哪種購買方案可使總費用最低?最低費用是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b的圖象l與坐標軸分別交于點E,F,與雙曲線y=﹣ ![]() (x<0)交于點P(﹣1,n),且F是PE的中點,直線x=a與l交于點A,與雙曲線交于點B(不同于A),PA=PB,則a= .
(x<0)交于點P(﹣1,n),且F是PE的中點,直線x=a與l交于點A,與雙曲線交于點B(不同于A),PA=PB,則a= . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市對初二綜合素質測評中的審美與藝術進行考核,規定如下:考核綜合評價得分由測試成績(滿分100分)和平時成績(滿分100分)兩部分組成,其中測試成績占80%,平時成績占20%,并且當綜合評價得分大于或等于80分時,該生綜合評價為A等.
(1)孔明同學的測試成績和平時成績兩項得分之和為185分,而綜合評價得分為91分,則孔明同學測試成績和平時成績各得多少分?
(2)某同學測試成績為70分,他的綜合評價得分有可能達到A等嗎?為什么?
(3)如果一個同學綜合評價要達到A等,他的測試成績至少要多少分?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,方格紙中的每個小方格都是邊長為1個單位的正方形,在建立平面直角坐標系后,點A,B,C均在格點上.
(1)請值接寫出點A,B,C的坐標.
(2)若平移線段AB,使B移動到C的位置,請在圖中畫出A移動后的位置D,依次連接B,C,D,A,并求出四邊形ABCD的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分線與AB的垂直平分線交于點O,將∠C沿EF(E在BC上,F在AC上)折疊,點C與點O恰好重合,則∠OEC的度數是( )
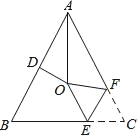
A. 106°B. 108°C. 110°D. 112°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的頂點P是BC中點,兩邊PE,PF分別交AB,AC于點E,F,給出以下五個結論:
①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤S四邊形AEPF= ![]() S△ABC .
S△ABC .
當∠EPF在△ABC內繞頂點P旋轉時(點E不與A,B重合),上述結論中始終正確的序號有 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為加強中小學生體育運動,某市第十七屆中小學生田徑運動會在市體育場舉行,體育場主席臺側面如圖所示,若頂棚頂端D與看臺底端A的連線和地面垂直,測得頂棚CD的長為12米,∠BAC=30°,∠ACD=45°,求看臺AC的長.(結果保留一位小數,參考數據: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)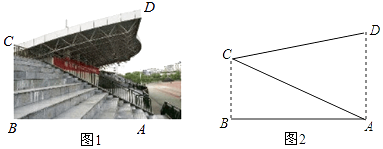
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com