
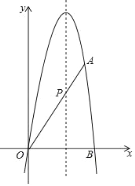
【題目】拋物線y=﹣![]() x2+bx+c(b,c均是常數(shù))經(jīng)過點O(0,0),A(4,4
x2+bx+c(b,c均是常數(shù))經(jīng)過點O(0,0),A(4,4![]() ),與x軸的另一交點為點B,且拋物線對稱軸與線段OA交于點P.
),與x軸的另一交點為點B,且拋物線對稱軸與線段OA交于點P.
(1)求該拋物線的解析式和頂點坐標;
(2)過點P作x軸的平行線l,若點Q是直線上的動點,連接QB.
①若點O關于直線QB的對稱點為點C,當點C恰好在直線l上時,求點Q的坐標;
②若點O關于直線QB的對稱點為點D,當線段AD的長最短時,求點Q的坐標(直接寫出答案即可).
【答案】(1)y=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ;(
;(![]() ,
,![]() );(2)①(﹣
);(2)①(﹣![]() ,
,![]() )或(
)或(![]() ,
,![]() );②(0,
);②(0,![]() );
);
【解析】
1)把0(0,0),A(4,4v3)的坐標代入
y=﹣![]() x2+bx+c,轉化為解方程組即可.
x2+bx+c,轉化為解方程組即可.
(2)先求出直線OA的解析式,點B坐標,拋物線的對稱軸即可解決問題.
(3)①如圖1中,點O關于直線BQ的對稱點為點C,當點C恰好在直線l上時,首先證明四邊形BOQC是菱形,設Q(m,![]() ),根據(jù)OQ=OB=5,可得方程
),根據(jù)OQ=OB=5,可得方程![]() ,解方程即可解決問題.
,解方程即可解決問題.
②如圖2中,由題意點D在以B為圓心5為半徑的OB上運動,當A,D、B共線時,線段AD最小,設OD與BQ交于點H.先求出D、H兩點坐標,再求出直線BH的解析式即可解決問題.
(1)把O(0,0),A(4,4![]() )的坐標代入y=﹣
)的坐標代入y=﹣![]() x2+bx+c,
x2+bx+c,
得![]() ,
,
解得![]() ,
,
∴拋物線的解析式為y=﹣![]() x2+5
x2+5![]() x=﹣
x=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() .
.
所以拋物線的頂點坐標為(![]() ,
,![]() );
);
(2)①由題意B(5,0),A(4,4![]() ),
),
∴直線OA的解析式為y=![]() x,AB=
x,AB=![]() =7,
=7,
∵拋物線的對稱軸x=![]() ,
,
∴P(![]() ,
,![]() ).
).
如圖1中,點O關于直線BQ的對稱點為點C,當點C恰好在直線l上時,
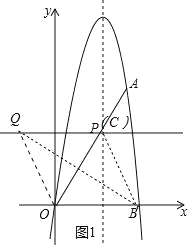
∵QC∥OB,
∴∠CQB=∠QBO=∠QBC,
∴CQ=BC=OB=5,
∴四邊形BOQC是平行四邊形,
∵BO=BC,
∴四邊形BOQC是菱形,
設Q(m,![]() ),
),
∴OQ=OB=5,
∴m2+(![]() )2=52,
)2=52,
∴m=±![]() ,
,
∴點Q坐標為(﹣![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
②如圖2中,由題意點D在以B為圓心5為半徑的⊙B上運動,當A、D、B共線時,線段AD最小,設OD與BQ交于點H.
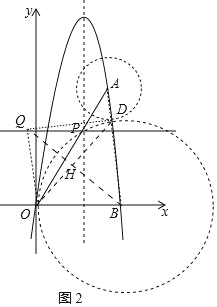
∵AB=7,BD=5,
∴AD=2,D(![]() ,
,![]() ),
),
∵OH=HD,
∴H(![]() ,
,![]() ),
),
∴直線BH的解析式為y=﹣![]() x+
x+![]() ,
,
當y=![]() 時,x=0,
時,x=0,
∴Q(0,![]() ).
).


 亮點激活精編提優(yōu)100分大試卷系列答案
亮點激活精編提優(yōu)100分大試卷系列答案 智趣寒假作業(yè)云南科技出版社系列答案
智趣寒假作業(yè)云南科技出版社系列答案科目:初中數(shù)學 來源: 題型:
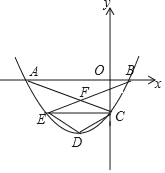
【題目】如圖,拋物線y=mx2+2mx+n經(jīng)過A(﹣3,0),C(0,﹣![]() )兩點,與x軸交于另一點B.
)兩點,與x軸交于另一點B.
(1)求經(jīng)過A,B,C三點的拋物線的解析式;
(2)過點C作CE∥x軸交拋物線于點E,寫出點E的坐標,并求AC、BE的交點F的坐標
(3)若拋物線的頂點為D,連結DC、DE,四邊形CDEF是否為菱形?若是,請證明;若不是,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某班將舉行“數(shù)學知識競賽”活動,班長安排小明購買獎品,下面兩圖是小明買回獎品時與班長的對話情境:

請根據(jù)上面的信息,解決問題:
(1)試計算兩種筆記本各買了多少本?
(2)請你解釋:小明為什么不可能找回68元?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】為了進一步了解某校初中學生的體質健康狀況,對八年級的部分學生進行了體質監(jiān)測,同時統(tǒng)計了每個人的得分(假設這個得分為![]() ,滿分為50分).體質檢測的成績分為四個等級:優(yōu)秀
,滿分為50分).體質檢測的成績分為四個等級:優(yōu)秀![]() 、良好
、良好![]() 、合格
、合格![]() 、不合格
、不合格![]() .根據(jù)調查結果繪制了下列兩福不完整的統(tǒng)計圖,請你根據(jù)統(tǒng)計圖提供的信息回答以下問題:
.根據(jù)調查結果繪制了下列兩福不完整的統(tǒng)計圖,請你根據(jù)統(tǒng)計圖提供的信息回答以下問題:
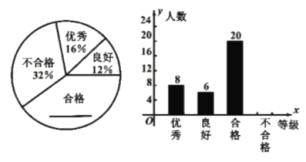
(1)補全上面的扇形統(tǒng)計圖和條形統(tǒng)計圖;
(2)被測試的部分八年級學生的體質測試成績的中位數(shù)落在 等級:
(3)若該校八年級有1400名學生,估計該校八年級體質為“不合格”的學生約有多少人?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知拋物線y=x2+bx+c的對稱軸為x=2,且過點C(0,3)
(1)求此拋物線的解析式;
(2)證明:該拋物線恒在直線y=﹣2x+1上方.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,以斜邊AB上一點O為圓心,OB為半徑作⊙O,交AC于點E,交AB于點D,且∠BEC=∠BDE.
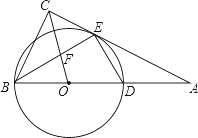
(1)求證:AC是⊙O的切線;
(2)連接OC交BE于點F,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在某小學“演講大賽”選拔賽初賽中,甲、乙、丙三位評委對小選手的綜合表現(xiàn),分別給出“待定”(用字母W表示)或“通過”(用字母P表示)的結論.
(1)請用樹狀圖表示出三位評委給小選手琪琪的所有可能的結論;
(2)對于小選手琪琪,只有甲、乙兩位評委給出相同結論的概率是多少?
(3)比賽規(guī)定,三位評委中至少有兩位給出“通過”的結論,則小選手可入圍進入復賽,問琪琪進入復賽的概率是多少?
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com