
【題目】如圖,△ABC是等邊三角形,DE∥AB分別交BC、AC于點D、E,過點E做EF⊥DE,交線段BC的延長線于點F。
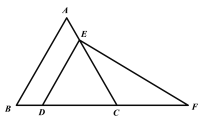
(1)求證:CE=CF;
(2)若BD=![]() CE,AB=8,求線段DF的長。
CE,AB=8,求線段DF的長。
【答案】(1)見解析(2)12
【解析】
(1)根據△ABC是等邊三角形得到∠ABC=∠A=∠ACB=60°,根據DE∥AB得到∠DEC=∠EDC=60°,故∠CEF=30°,∠F=90°-∠EDC=30°,則∠F=∠CEF,問題得證;
(2)先證明△DCE為等邊三角形,根據BD=![]() CE=
CE=![]() CD,故BD=
CD,故BD=![]() BC,CF=CE=CD=
BC,CF=CE=CD=![]() BC=
BC=![]() AB,故可求解.
AB,故可求解.
(1)∵△ABC是等邊三角形
∴∠ABC=∠A=∠ACB=60°,
∵DE∥AB
∴∠DEC=∠EDC=60°,
∵EF⊥DE,
∴∠CEF=90°-∠DEC=30°,∠F=90°-∠EDC=30°,
∴∠F=∠CEF
∴CE=CF
(2)∵∠DEC=∠EDC=60°
∴△DCE為等邊三角形,
∵BD=![]() CE=
CE=![]() CD,
CD,
∴BD=![]() BC,
BC,
∴CF=CE=CD=![]() BC=
BC=![]() AB=6,
AB=6,
∴DF=CF+DC=12.


科目:初中數學 來源: 題型:
【題目】某人駕車從![]() 地出發在一條筆直的南北方向上來回行駛,向北行駛為正,向南行駛為負,行駛的路程情況如下(單位:千米):
地出發在一條筆直的南北方向上來回行駛,向北行駛為正,向南行駛為負,行駛的路程情況如下(單位:千米):![]() .
.
![]() 該人在完成上述
該人在完成上述![]() 次行車后在
次行車后在![]() 地的哪一側?距
地的哪一側?距![]() 地多少千米?
地多少千米?
![]() 如果這輛車每行駛
如果這輛車每行駛![]() 千米的耗油量為
千米的耗油量為![]() 升,這一天共耗油多少升?
升,這一天共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,在△ABC中,∠ACB=90°,AC=BC,直線l過點C,點A,B在直線l同側,BD⊥l,AE⊥l,垂足分別為D,E.求證:△AEC≌△CDB.
(2)如圖2,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,利用(1)中的結論,請按照圖中所標注的數據計算圖中實線所圍成的圖形的面積S= .

查看答案和解析>>
科目:初中數學 來源: 題型:
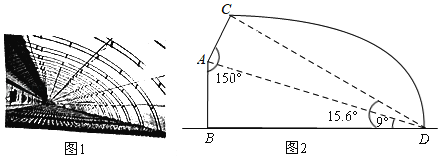
【題目】隨著我市農產品整體品牌形象“聊勝一籌!”的推出,現代農業得到了更快發展.某農場為擴大生產建設了一批新型鋼管裝配式大棚,如圖1.線段AB,BD分別表示大棚的墻高和跨度,AC表示保溫板的長.已知墻高AB為2米,墻面與保溫板所成的角∠BAC=150°,在點D處測得A點、C點的仰角分別為9°,15.6°,如圖2.求保溫板AC的長是多少米?(精確到0.1米)
(參考數據:![]() ≈0.86,sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28)
≈0.86,sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在坐標平面內,點O是坐標原點,A(0,6)、B(2![]() ,0),且∠OBA=60°,將△OAB沿直線AB翻折,得到△CAB,點O與點C對應。
,0),且∠OBA=60°,將△OAB沿直線AB翻折,得到△CAB,點O與點C對應。
(1)求點C的坐標;
(2)動點F從點O出發,以2個單位長度/秒的速度沿折線O—A—C向終點C運動,設△FOB的面積為S(S≠0),點F的運動時間為t秒,求S與t的關系式,并直接寫出t的取值范圍;
(3)在(2)的條件下,過點B作x軸垂線,交AC于點E,在點F的運動過程中,當t為何值時,△BEF是以BE為腰的等腰三角形?

查看答案和解析>>
科目:初中數學 來源: 題型:
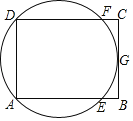
【題目】如圖,矩形ABCD中,G是BC的中點,過A、D、G三點的圓O與邊AB、CD分別交于點E、點F,給出下列說法:(1)AC與BD的交點是圓O的圓心;(2)AF與DE的交點是圓O的圓心;(3)BC與圓O相切,其中正確說法的個數是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
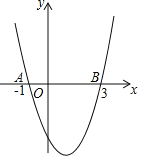
【題目】如圖,二次函數y=ax2+bx+c的圖象與x軸交于點A(﹣1,0),B(3,0).下列結論:①2a﹣b=0;②(a+c)2<b2;③當﹣1<x<3時,y<0;④當a=1時,將拋物線先向上平移2個單位,再向右平移1個單位,得到拋物線y=(x﹣2)2﹣2.其中正確的是( )
A. ①③ B. ②③ C. ②④ D. ③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com