【題目】下列小金魚圖案是用長度相同的小木棒按一定規律拼搭而成，第一條小金魚圖案需8根小木棒，第二條小金魚圖案需14根小木棒，…，按此規律，
（1）第n條小金魚圖案需要小木棒 根；
（2）如果有30000根小木棒，按照如圖所示拼搭第1條，第2條……，直到第100條金魚，請通過計算說明這些木棒是否夠用．
【答案】（1）（6n+2）；（2）這些木棒不夠用，理由詳見解析．
【解析】
（1）根據圖形的變化，先求出前幾個圖案所需小木棒的根數，由此發現規律，總結規律；
（2）根據（1）所得規律，進行計算即可說明這些木棒是否夠用．
解：（1）第一條小金魚圖案需8根小木棒，即8＝6×1+2；
第二條小金魚圖案需14根小木棒，即14＝6×2+2；
第三條小金魚圖案需20根小木棒，即20＝6×3+2
…，
發現規律，
第n條小金魚圖案需要小木棒（6n+2）根；
故答案為：（6n+2）；
（2）拼搭第1條，第2條……，直到第100條金魚，
所需小木棒：8+14+20+…+602
＝
＝30500＞30000．
答：這些木棒不夠用．
手拉手全優練考卷系列答案科目：初中數學 來源： 題型：
【題目】閱讀下列一段文字：在直角坐標系中，已知兩點的坐標是M（x1，y1），N（x2，y2）），M，N兩點之間的距離可以用公式MN＝
計算．解答下列問題：
（1）若點P（2，4），Q（﹣3，﹣8），求P，Q兩點間的距離；
（2）若點A（1，2），B（4，﹣2），點O是坐標原點，判斷△AOB是什么三角形，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：在△ABC中,∠ABC=60°,CD平分∠ACB交AB于點D,點E在線段CD上(點E不與點C. D重合)，且∠EAC=2∠EBC.
(1)如圖1,若∠EBC=27°,且EB=EC,則∠DEB=___°,∠AEC=___°.
(2)如圖2，①求證：AE+AC=BC；
②若∠ECB=30°，且AC=BE，求∠EBC的度數。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】數學課上小明用一副三角板進行如下操作：把一副三角板中兩個直角的頂點重合，一個三角板固定不動，另一個三角板繞著重合的頂點旋轉（兩個三角板始終有重合部分）．
（1）當旋轉到如圖所示的位置時，量出∠α＝25°，通過計算得出∠AOD＝∠BOC＝ ；
（2）通過幾次操作小明發現，∠α≠25°時．∠AOD＝∠BOC仍然成立，請你幫他完成下面的說理過程．
理由：因為∠AOC＝∠BOD＝ ；
所以，根據等式的基本性質∠ ﹣∠COD＝∠BOD﹣∠ ；
即∠AOD＝∠ ．
（3）小瑩還發現在旋轉過程中∠AOB和∠DOC之間存在一個不變的數量關系，請你用等式表示這個數量關系 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，平面直角坐標系中，點A是x軸負半軸上一個定點，點P是函數
上一個動點，
軸于點B，當點P的橫坐標逐漸增大時，四邊形OAPB的面積將會
A. 先增后減 B. 先減后增 C. 逐漸減小 D. 逐漸增大
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，AC∥BD，請先作圖再解決問題．
(1)利用尺規完成以下作圖，并保留作圖痕跡．(不要求寫作法)
①作BE平分∠ABD交AC于點E；
②在BA的延長線上截取AF=BA，連接EF；
(2)判斷△BEF的形狀，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
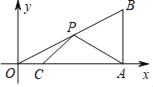
【題目】如圖，在平面直角坐標系中，Rt△OAB的直角頂點A在x軸的正半軸上，頂點B的坐標為（3，
），點C的坐標為（1，0），且∠B=60°，點P為斜邊OB上的一個動點，則PA+PC的最小值為_____．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
