
【題目】菱形![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 上一個動點,
上一個動點,![]() ,連接
,連接![]() 并延長交
并延長交![]() 延長線于點
延長線于點![]() .
.
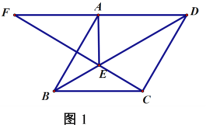
(1)如圖1,求證:![]() ;
;
(2)當![]() 為直角三角形時,求
為直角三角形時,求![]() 的長;
的長;
(3)當![]() 為
為![]() 的中點,求
的中點,求![]() 的最小值.
的最小值.
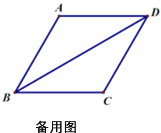
【答案】(1)詳見解析;(2)當![]() 為直角三角形時,
為直角三角形時,![]() 的長是
的長是![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)先根據(jù)菱形的性質(zhì)證![]() ,再證
,再證![]() ,由全等的性質(zhì)可得
,由全等的性質(zhì)可得![]() ,進而得出結論;
,進而得出結論;
(2)分以下兩種情況討論:①![]() ,②
,②![]() ;
;
(3)過![]() 作
作![]() 于
于![]() ,過
,過![]() 作
作![]() 于
于![]() ,當
,當![]() 三點在同一直線上且
三點在同一直線上且![]() 時
時![]() 的值最小,即為
的值最小,即為![]() 的長.
的長.
解:(1)![]() 四邊形
四邊形![]() 是菱形,
是菱形,
![]() ,
,![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
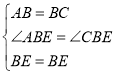
![]() ,
,
![]() ,
,
![]() .
.
(2)連接![]() 交
交![]() 于點
于點![]() ,
,

![]() 四邊形
四邊形![]() 是菱形,
是菱形,
![]() ,
,![]() .
.
又∠ABC=60°,∴△ABC為等邊三角形,
∴![]() ,
,![]() .
.
∴![]()
![]() .
.
∴![]() .
.
![]() ,
,
![]() .
.
當![]() 時,有
時,有![]() ,
,
在![]() 中,
中,
![]() ,
,
![]() 設
設![]() ,
,![]() ,
,
![]() ,
,
![]() ,解得
,解得![]() .
.
![]() .
.
![]() .
.
當![]() 時,有
時,有![]() ,
,
由![]() 知
知![]() ,
,
![]() 是等腰直角三角形.
是等腰直角三角形.
![]()
![]() .
.
綜上:當![]() 為直角三角形時,
為直角三角形時,![]() 的長是
的長是![]() 或
或![]() .
.
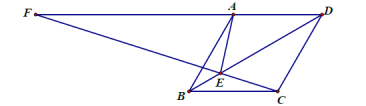
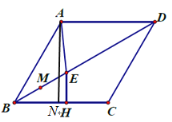
(3)過![]() 作
作![]() 于
于![]() ,過
,過![]() 作
作![]() 于
于![]() ,
,
在![]() 中,
中,
![]()
![]()
又![]() 是
是![]() 的中點,
的中點,![]()
![]()
![]() .
.
當![]() 三點在同一直線上且
三點在同一直線上且![]() 時
時
![]() 的值最小,即為
的值最小,即為![]() 的長.
的長.
在![]() 中,
中,
![]() ,
,![]() ,
,
![]() ,
,
∴![]() .
.
![]() 的最小值是
的最小值是![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,等邊△ABC的邊長為4,AD是BC邊上的中線,F是AD邊上的動點,E是AC邊上一點,若AE=2,當EF+CF取得最小值時,則∠BCF的度數(shù)為_____.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖(1)是某河上一座古拱橋的截面圖,拱橋橋洞上沿是拋物線形狀,拋物線兩端點與水面的距離都是1m,拱橋的跨度為10m,橋洞與水面的最大距離是5m,橋洞兩側壁上各有一盞距離水面4m的景觀燈.現(xiàn)把拱橋的截面圖放在平面直角坐標系中,如圖(2).


求(1)拋物線的解析式;
(2)兩盞景觀燈P1、P2之間的水平距離.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】(題文)
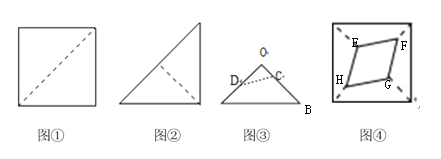
將一張正方形紙片按如圖步驟①②,沿虛線對折2次,然后沿圖③的虛線剪去一個角,展開鋪平后得到圖④,若圖③中![]() ,
,![]() ,則四邊形
,則四邊形![]() 與原正方形紙面積比為( )
與原正方形紙面積比為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】(2011內(nèi)蒙古赤峰,7,3分)早晨,小張去公園晨練,下圖是他離家的距離y(千
米)與時間t(分鐘)的函數(shù)圖象,根據(jù)圖象信息,下列說法正確的是 ( )

A.小張去時所用的時間多于回家所用的時間B.小張在公園鍛煉了20分鐘
C.小張去時的速度大于回家的速度 D.小張去時走上坡路,回家時走下坡路
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
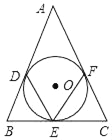
【題目】如圖,△ABC的三邊分別切⊙O于D,E,F(xiàn).
(1)若∠A=40°,求∠DEF的度數(shù);
(2)AB=AC=13,BC=10,求⊙O的半徑.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】甲乙兩位老師同住一小區(qū),該小區(qū)與學校相距![]() 米.甲從小區(qū)步行去學校,出發(fā)
米.甲從小區(qū)步行去學校,出發(fā)![]() 分鐘后乙再出發(fā),乙從小區(qū)先騎公共自行車,騎行若干米到達還車點后,立即步行走到學校.已知乙騎車的速度為
分鐘后乙再出發(fā),乙從小區(qū)先騎公共自行車,騎行若干米到達還車點后,立即步行走到學校.已知乙騎車的速度為![]() 米/分,甲步行的速度比乙步行的速度每分鐘快
米/分,甲步行的速度比乙步行的速度每分鐘快![]() 米.設甲步行的時間為
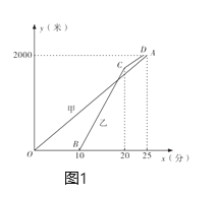
米.設甲步行的時間為![]() (分),圖1中線段
(分),圖1中線段![]() 與折線
與折線![]() 分別表示甲、乙離小區(qū)的路程
分別表示甲、乙離小區(qū)的路程![]() (米)與甲步行時間
(米)與甲步行時間![]() (分)的函數(shù)關系的圖象;圖2表示甲、乙兩人之間的距離
(分)的函數(shù)關系的圖象;圖2表示甲、乙兩人之間的距離![]() (米)與甲步行時間
(米)與甲步行時間![]() (分)的函數(shù)關系的圖象(不完整),根據(jù)圖1和圖2中所給的信息,解答下列問題:
(分)的函數(shù)關系的圖象(不完整),根據(jù)圖1和圖2中所給的信息,解答下列問題:
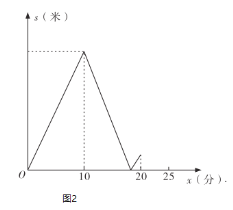
(1)求甲步行的速度和乙出發(fā)時甲離開小區(qū)的路程;
(2)求直線![]() 的解析式;
的解析式;
(3)在圖2中,畫出當![]() 時,
時,![]() 關于
關于![]() 的函數(shù)的大致圖象.
的函數(shù)的大致圖象.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖1,已知正方形ABCD的邊CD在正方形DEFG的邊DE上,連接AE,GC.
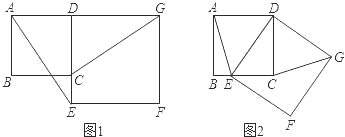
(1)試猜想AE與GC有怎樣的位置關系,并證明你的結論;
(2)將正方形DEFG繞點D按順時針方向旋轉,使點E落在BC邊上,如圖2,連接AE和GC.你認為(1)中的結論是否還成立?若成立,給出證明;若不成立,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com