
【題目】如圖,反比例函數y= ![]() (x>0)的圖象與邊長為5的等邊△AOB的邊OA,AB分別相交于C,D兩點,若OC=2BD,則實數k的值為( )
(x>0)的圖象與邊長為5的等邊△AOB的邊OA,AB分別相交于C,D兩點,若OC=2BD,則實數k的值為( ) 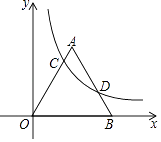
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:過點C作CE⊥x軸于點E,過點D作DF⊥x軸于點F, 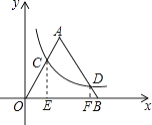
設OC=2x,則BD=x,
在Rt△OCE中,∠COE=60°,
則OE=x,CE= ![]() x,
x,
則點C坐標為(x, ![]() x),
x),
在Rt△BDF中,BD=x,∠DBF=60°,
則BF= ![]() x,DF=
x,DF= ![]() x,
x,
則點D的坐標為(5﹣ ![]() x,
x, ![]() x),
x),
將點C的坐標代入反比例函數解析式可得:k= ![]() x2 ,
x2 ,
將點D的坐標代入反比例函數解析式可得:k= ![]() x﹣
x﹣ ![]() x2 ,
x2 ,
則 ![]() x2=
x2= ![]() x﹣
x﹣ ![]() x2 ,
x2 ,
解得:x1=2,x2=0(舍去),
故k= ![]() x2=
x2= ![]() ×4=4
×4=4 ![]() .
.
故選A.
【考點精析】解答此題的關鍵在于理解等邊三角形的性質的相關知識,掌握等邊三角形的三個角都相等并且每個角都是60°.


科目:初中數學 來源: 題型:
【題目】如圖,一次函數y1=kx+b的圖象與反比例函數y2= ![]() 的圖象相交于點A(2,3)和點B,與x軸相交于點C(8,0).
的圖象相交于點A(2,3)和點B,與x軸相交于點C(8,0). 
(1)求這兩個函數的解析式;
(2)當x取何值時,y1>y2 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=2,AB=3,把梯形ABCD分別繞直線AB,CD旋轉一周,所得幾何體的表面積分別為S1 , S2 , 則|S1﹣S2|=(平方單位) 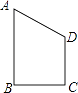
查看答案和解析>>
科目:初中數學 來源: 題型:
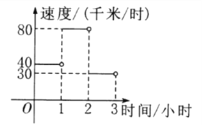
【題目】某人駕車從鄉(xiāng)村進城.各時間段的行駛速度如圖所示.當![]() 時,其行駛路程
時,其行駛路程![]() 與時間
與時間![]() 之間的函數表達式是________,當
之間的函數表達式是________,當![]() 時,其行駛路程
時,其行駛路程![]() 與時間
與時間![]() 之間的函數表達式是________,當
之間的函數表達式是________,當![]() 時,其行駛路程
時,其行駛路程![]() 與時間
與時間![]() 之間的函數表達式是________.
之間的函數表達式是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形OABC的頂點A、C分別在x、y軸的正半軸上,點D為對角線OB的中點,點E(4,n)在邊AB上,反比例函數 ![]() (k≠0)在第一象限內的圖象經過點D、E,且tan∠BOA=
(k≠0)在第一象限內的圖象經過點D、E,且tan∠BOA= ![]() .
.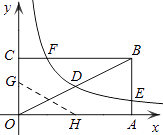
(1)求邊AB的長;
(2)求反比例函數的解析式和n的值;
(3)若反比例函數的圖象與矩形的邊BC交于點F,將矩形折疊,使點O與點F重合,折痕分別與x、y軸正半軸交于點H、G,求線段OG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義符號min{a,b}的含義為:當a≥b時min{a,b}=b;當a<b時min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.則min{﹣x2+1,﹣x}的最大值是( )
A.![]()
B.![]()
C.1
D.0
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,網格線的交點叫格點,格點P是∠AOB的邊OB上的一點(請利用網格作圖,保留作圖痕跡). 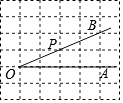
(1)過點P畫OB的垂線,交OA于點C;
(2)線段的長度是點O到PC的距離;
(3)PC<OC的理由是;
(4)過點C畫OB的平行線.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為開展體育大課間活動,需要購買籃球與足球若干個.已知購買2個籃球和3個足球共需要380元;購買4個籃球和5個足球共需要700元.
(1)求購買一個籃球、一個足球各需多少元?
(2)若體育老師帶了6000元去購買這種籃球與足球共80個.由于數量較多,店主給出“一律打九折”的優(yōu)惠價,那么他最多能購買多少個籃球?
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com