
【題目】每年的6月5日為世界環保日,為提倡低碳環保,某公司決定購買10臺節省能源的新機器,現有甲、乙兩種型號的機器可選,其中每臺的價格、產量如下表:
甲型機器 | 乙型機器 | |
價格(萬元/臺) | a | b |
產量(噸/月) | 240 | 180 |
經調查:購買一臺甲型機器比購買一臺乙型機器多12萬元,購買2臺甲型機器比購買3臺乙型機器多6萬元.
(1) 求a、b的值;
(2) 若該公司購買新機器的資金不超過216萬元,請問該公司有哪幾種購買方案?
(3) 在(2)的條件下,若公司要求每月的產量不低于1890噸,請你為該公司設計一 種最省錢的購買方案.
【答案】(1)![]() ;(2)有 4 種方案:3 臺甲種機器,7 臺乙種機器;2 臺甲種機器,8 臺乙種機器;1 臺甲種機器,9 臺乙種機器;
;(2)有 4 種方案:3 臺甲種機器,7 臺乙種機器;2 臺甲種機器,8 臺乙種機器;1 臺甲種機器,9 臺乙種機器;
10 臺乙種機器. (3)最省錢的方案是購買 2 臺甲種機器,8 臺乙種機器.
【解析】
(1)根據購買一臺甲型機器比購買一臺乙型機器多12萬元,購買2臺甲型機器比購買3臺乙型機器多6萬元這一條件建立一元二次方程組求解即可,(2)設買了x臺甲種機器,根據該公司購買新機器的資金不超過216萬元,建立一次不等式求解即可,(3)將兩種機器生產的產量相加,使總產量不低于1890噸,求出x的取值范圍,再分別求出對應的成本即可解題.
(1)解:由題意得![]() ,
,
解得,![]() ;
;
(2)解:設買了x臺甲種機器
由題意得:30+18(10-x)≤216
解得:x≤3
∵x為非負整數
∴x=0、1、2、3
∴有 4 種方案:
3 臺甲種機器,7 臺乙種機器;
2 臺甲種機器,8 臺乙種機器;
1 臺甲種機器,9 臺乙種機器;
10 臺乙種機器.
(3)解:由題意得:240+180(10-x)≥1890
解得:x≥1.5
∴1.5≤x≤ 3
∴整數 x=2 或 3
當 x=2 時購買費用=30×2+18×8=204(元)
當 x=3 時購買費用=30×3+18×7=216(元)
∴最省錢的方案是購買 2 臺甲種機器,8 臺乙種機器.


 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知點![]() 、點
、點![]() ,一次函數
,一次函數![]() 的圖象與直線AB交于點P.
的圖象與直線AB交于點P.
(1)求直線AB的函數表達式及P點的坐標;
(2)若點Q是y軸上一點,且△BPQ的面積為2,求點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個工程隊計劃參與一項工程建設,甲隊單獨施工![]() 天完成該項工程的
天完成該項工程的![]() ,這時乙隊加入,兩隊還需同時施工
,這時乙隊加入,兩隊還需同時施工![]() 天,才能完成該項工程.
天,才能完成該項工程.
(1)若乙隊單獨施工,需要多少天才能完成該項工程;
(2)若甲隊參與該項工程施工的時間不超過![]() 天,則乙隊至少施工多少天才能完成該項工程?
天,則乙隊至少施工多少天才能完成該項工程?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 在
在![]() 軸上,
軸上, ![]() ,將線段
,將線段![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() ,使點
,使點![]() 與點
與點![]() 重合.
重合.
(1)求點![]() 的坐標;
的坐標;
(2)求經過![]() 、
、![]() 、
、![]() 三點的拋物線的解析式;
三點的拋物線的解析式;
(3)在此拋物線的對稱軸上,是否存在點![]() ,使得以點
,使得以點![]() 、
、![]() 、
、![]() 為頂點的三角形是等腰三角形?若存在,求出點
為頂點的三角形是等腰三角形?若存在,求出點![]() 的坐標:若不存在,請說明理由.
的坐標:若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為改善辦學條件,計劃采購A、B兩種型號的空調,已知采購3臺A型空調和2臺B型空調,需費用39000元;4臺A型空調比5臺B型空調的費用多6000元.
(1)求A型空調和B型空調每臺各需多少元;
(2)若學校計劃采購A、B兩種型號空調共30臺,且A型空調的臺數不少于B型空調的一半,兩種型號空調的采購總費用不超過217000元,該校共有哪幾種采購方案?
(3)在(2)的條件下,采用哪一種采購方案可使總費用最低,最低費用是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
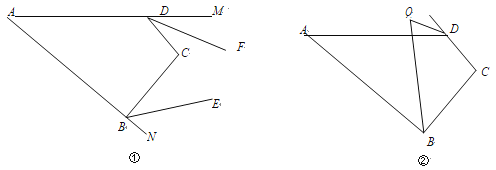
【題目】如圖①,在四邊形 ABCD 中,∠A=x°,∠C=y°.
(1) ∠ABC+∠ADC= °.(用含 x,y 的代數式表示)
(2) BE、DF 分別為∠ABC、∠ADC 的外角平分線,
①若 BE∥DF,x=30,則 y= ;
②當 y=2x 時,若 BE 與 DF 交于點 P,且∠DPB=20°,求 y 的值.
(3) 如圖②,∠ABC 的平分線與∠ADC 的外角平分線交于點 Q,則∠Q= °.(用含 x,y 的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠為了擴大生產,決定購買6臺機器用于生產零件,現有甲、乙兩種機器可供選擇.其中甲型機器每日生產零件106個,乙型機器每日生產零件60個,經調査,購買3臺甲型機器和2臺乙型機器共需要31萬元,購買一臺甲型機器比購買一臺乙型機器多2萬元
(1)求甲、乙兩種機器每臺各多少萬元?
(2)如果工廠期買機器的預算資金不超過34萬元,那么你認為該工廠有哪幾種購買方案?
(3)在(2)的條件下,如果要求該工廠購進的6臺機器的日產量能力不能低于380個,那么為了節約資金.應該選擇哪種方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(8分)在學習概率的課堂上,老師提出問題:只有一張電影票,小明和小剛想通過抽取撲克牌的游戲來決定誰去看電影,請你設計一個對小明和小剛都公平的方案.
甲同學的方案:將紅桃2、3、4、5四張牌背面向上,小明先抽一張,小剛從剩下的三張牌中抽一張,若兩張牌上的數字之和是奇數,則小明看電影,否則小剛看電影.
(1)甲同學的方案公平嗎?請用列表或畫樹狀圖的方法說明;
(2)乙同學將甲的方案修改為只用紅桃2、3、4三張牌,抽取方式及規則不變,乙的方案公平嗎?(只回答,不說明理由)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com