
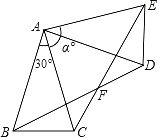
【題目】如圖,△ABC中,AB=AC,∠BAC=30°,將△ABC繞點(diǎn)A按逆時(shí)針?lè)较蛐D(zhuǎn)α°.得到△ADE,連接BD,CE交于點(diǎn)F.
(1)求證:△ABD≌△ACE;
(2)用α表示∠ACE的度數(shù);
(3)若使四邊形ABFE是菱形,求α的度數(shù).
【答案】(1)證明見(jiàn)解析;(2)∠ACE==90°﹣![]() ;(3)120°.
;(3)120°.
【解析】
(1)根據(jù)旋轉(zhuǎn)角求出∠BAD=∠CAE,然后利用“邊角邊”證明△ABD和△ACE全等;
(2)根據(jù)等腰三角形的性質(zhì)得到結(jié)論;
(3)根據(jù)等腰三角形的性質(zhì)得到∠ABD=∠ADB=∠ACE=∠AEC=90°﹣![]() ,求得∠BFE=150°,若使四邊形ABFE是菱形,只要四邊形ABFE是平行四邊形即可,得到∠BAE=∠BFE,于是得到結(jié)論.
,求得∠BFE=150°,若使四邊形ABFE是菱形,只要四邊形ABFE是平行四邊形即可,得到∠BAE=∠BFE,于是得到結(jié)論.
解:(1)證明:∵ABC繞點(diǎn)A按逆時(shí)針?lè)较蛐D(zhuǎn)α°,
∴∠BAC=∠DAE=30°,∠BAD=∠CAE=α°,
又∵AB=AC,
∴AB=AC=AD=AE,
在△ABD與△ACE中,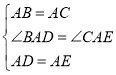 ,
,
∴△ABD≌△ACE(SAS);
(2)解:∵∠CAE=α°,AC=AE,
∴∠ACE=![]() (180°﹣∠CAE)=
(180°﹣∠CAE)=![]() (180°﹣α°)=90°﹣
(180°﹣α°)=90°﹣![]() ;
;
(3)解:∵∠BAD=∠CAE=α°,AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=90°﹣![]() ,
,
∵∠BAE=∠BAD+∠DAE=α°+30°=(α+30)°,
∴∠BFE=360°﹣∠BAE﹣∠ABD﹣∠AEC=360°﹣(α+30)°﹣2(90°﹣![]() )=150°,
)=150°,
∵AB=AE,
∴若使四邊形ABFE是菱形,
只要四邊形ABFE是平行四邊形即可,
∵∠ABD=∠AEC,
∴只要∠BAE=∠BFE,
即(30+α)°=150°,
解得:α°=120°,
即當(dāng)α°=120°時(shí),四邊形ABFE是菱形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
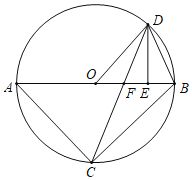
【題目】如圖,已知△ABC內(nèi)接于⊙O,AB是直徑,點(diǎn)D在⊙O上,OD∥BC,過(guò)點(diǎn)D作DE⊥AB,垂足為E,連接CD交OE邊于點(diǎn)F.
(1)求證:△DOE∽△ABC;
(2)求證:∠ODF=∠BDE;
(3)連接OC.設(shè)△DOE的面積為S.sinA=![]() ,求四邊形BCOD的面積(用含有S的式子表示)
,求四邊形BCOD的面積(用含有S的式子表示)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
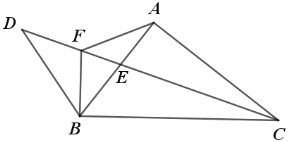
【題目】如圖,Rt△ABC 中,∠BAC=90°,CE 平分∠ACB,點(diǎn) D 在 CE的延長(zhǎng)線上,連接 BD,過(guò)B作BF⊥BC交 CD 于點(diǎn) F,連接 AF,若CF=2BD ,DE:CE=5:8 , BF ![]() ,則AF的長(zhǎng)為_________.
,則AF的長(zhǎng)為_________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】疫情期間,“線上教學(xué)”為我們提供了復(fù)習(xí)的渠道.學(xué)校隨機(jī)抽取部分學(xué)生就“你是否喜歡線上教學(xué)”進(jìn)行了問(wèn)卷調(diào)查,并將調(diào)查結(jié)果統(tǒng)計(jì)后繪制成如下統(tǒng)計(jì)表和統(tǒng)計(jì)圖.
調(diào)查結(jié)果統(tǒng)計(jì)表
類別 | 非常喜歡 | 喜歡 | 一般 | 不喜歡 |
頻數(shù) | a | 70 | 20 | 10 |
頻率 | 0.5 | b | 0.15 | |
調(diào)查結(jié)果扇形統(tǒng)計(jì)圖

(1)在統(tǒng)計(jì)表中,a= ;b= ;
(2)在扇形統(tǒng)計(jì)圖中,對(duì)線上教學(xué)感覺(jué)“一般”所對(duì)應(yīng)的圓心角度數(shù)為 ;
(3)已知全校共有3000名學(xué)生,試估計(jì)“喜歡”線上教學(xué)的學(xué)生人數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】有一邊長(zhǎng)為10m的等邊△ABC游樂(lè)場(chǎng),某人從邊AB中點(diǎn)P出發(fā),先由點(diǎn)P沿平行于BC的方向運(yùn)動(dòng)到AC邊上的點(diǎn)P1,再由P1沿平行于AB方向運(yùn)動(dòng)到BC邊上的點(diǎn)P2,又由點(diǎn)P2沿平行于AC方向運(yùn)動(dòng)到AB邊上的點(diǎn)P3,則此人至少要運(yùn)動(dòng)_____m,才能回到點(diǎn)P.如果此人從AB邊上任意一點(diǎn)出發(fā),按照上面的規(guī)律運(yùn)動(dòng),則此人至少走_____m,就能回到起點(diǎn).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
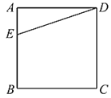
【題目】正方形![]() 中,點(diǎn)
中,點(diǎn)![]() 在邊
在邊![]() 上,
上,![]() ,
,![]() ,將線段
,將線段![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn),使點(diǎn)
逆時(shí)針旋轉(zhuǎn),使點(diǎn)![]() 落在直線
落在直線![]() 上E的點(diǎn)
上E的點(diǎn)![]() 處,則
處,則![]() 的長(zhǎng)度為______.
的長(zhǎng)度為______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】對(duì)于平面直角坐標(biāo)系![]() 中的圖形
中的圖形![]() ,
,![]() ,給出如下定義:
,給出如下定義:![]() 為圖形
為圖形![]() 上任意一點(diǎn),
上任意一點(diǎn),![]() 為圖形
為圖形![]() 上任意一點(diǎn),如果線段
上任意一點(diǎn),如果線段![]() 的長(zhǎng)度有最小值,那么稱這個(gè)最小值為圖形
的長(zhǎng)度有最小值,那么稱這個(gè)最小值為圖形![]() ,
,![]() 的“近距”,記作
的“近距”,記作![]() ;如果線段
;如果線段![]() 的長(zhǎng)度有最大值,那么稱這個(gè)最大值為圖形
的長(zhǎng)度有最大值,那么稱這個(gè)最大值為圖形![]() ,
,![]() 的“遠(yuǎn)距”,記作
的“遠(yuǎn)距”,記作![]() .
.
已知點(diǎn)![]() ,
,![]() .
.
(1)![]() (點(diǎn)
(點(diǎn)![]() ,線段
,線段![]() )
)![]() ______,
______,![]() (點(diǎn)
(點(diǎn)![]() ,線段
,線段![]() )
)![]() ______;
______;
(2)一次函數(shù)![]() 的圖象與
的圖象與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,與
,與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,若
,若![]() (線段
(線段![]() ,線段
,線段![]() )
)![]() ,
,
①求![]() 的值;
的值;
②直接寫(xiě)出![]() (線段
(線段![]() ,線段
,線段![]() )
)![]() ______;
______;
(3)![]() 的圓心為
的圓心為![]() ,半徑為1.若
,半徑為1.若![]() (
(![]() 線段
線段![]() )
)![]() ,請(qǐng)直接寫(xiě)出
,請(qǐng)直接寫(xiě)出![]() (
(![]() ,線段
,線段![]() )的取值范圍.
)的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
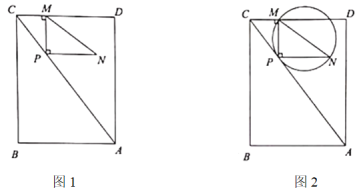
【題目】如圖1,直角三角形![]() 的直角頂點(diǎn)
的直角頂點(diǎn)![]() 在矩形
在矩形![]() 的對(duì)角線
的對(duì)角線![]() 上(點(diǎn)
上(點(diǎn)![]() 不與點(diǎn)
不與點(diǎn)![]() 重合,可與點(diǎn)
重合,可與點(diǎn)![]() 重合),滿足
重合),滿足![]() ,
,![]() 于點(diǎn)
于點(diǎn)![]() ,已知
,已知![]() ,
,![]() .
.
(1)若![]() ,則
,則![]() ___________;
___________;
(2)當(dāng)點(diǎn)![]() 在
在![]() 的平分線上時(shí),求
的平分線上時(shí),求![]() 的長(zhǎng);
的長(zhǎng);
(3)當(dāng)點(diǎn)![]() 的位置發(fā)生改變時(shí):
的位置發(fā)生改變時(shí):
①如圖2,![]() 的外接圓是否與
的外接圓是否與![]() 一直保持相切.說(shuō)明理由;
一直保持相切.說(shuō)明理由;
②直接寫(xiě)出![]() 的外接圓與
的外接圓與![]() 相切時(shí)
相切時(shí)![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于點(diǎn)E.在△ABC外有一點(diǎn)F,使FA⊥AE,F(xiàn)C⊥BC.
(1)求證:BE=CF;
(2)在AB上取一點(diǎn)M,使BM=2DE,連接MC,交AD于點(diǎn)N,連接ME.求證:①ME⊥BC;②DE=DN.

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com