Question

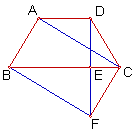
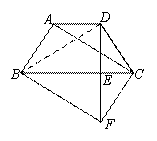
如圖，在梯形ABCD中，AD∥BC，AB＝DC，過點D作DE⊥BC，垂足為E，并延長DE至F，使EF＝DE．聯(lián)結BF，CF，AC．

（1）求證：四邊形ABFC是平行四邊形；

（2）如果DE²＝BE·CE，求證四邊形ABFC是矩形．

 

Answer 1

（1）連接BD．                      　　　　         …………………………1分

∵DE⊥BC，EF＝DE，

∴BD＝BF，CD＝CF．                　　　　                     …………2分

∵在梯形ABCD中，AD//BC，AB＝DC，

∴四邊形ABCD是等腰梯形．

∴BD＝AC．                       　　　　                       …………3分

∴AC＝BF，AB＝CF．

∴四邊形ABFC是平行四邊形．         　　　　                      ………4分

（2）∵DE² ＝BE·CE，EF＝DE，∴EF² ＝BE·CE．∴．　　　　……6分

又∵DE⊥BC，∴∠CEF＝∠FEB＝90°．∴△CEF∽△FEB．∴∠CFE＝∠FBE．∵∠FBE＋∠BFE＝90°，∴∠CFE ＋∠BFE＝90°．即∠BFC＝90°．    　　　   …………7分

由（1）知四邊形ABFC是平行四邊形，∴四邊形ABFC是矩形．　　　　…………8分