【題目】如圖所示，在正方形ABCD中，M為AB的中點，N為AD上的一點，且AN= 
AD，試猜測△CMN是什么三角形，請證明你的結論．（提示：正方形的四條邊都相等，四個角都是直角） 
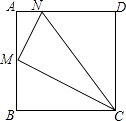
【答案】解：△CMN是直角三角形．理由如下： 設正方形ABCD的邊長為4a，則AB=BC=CD=AD=4a．
∵M是AB的中點，
∴AM=BM=2a．
∵AN= 
AD，AD=4a，
∴AN=a，DN=3a．
∵在Rt△AMN中，滿足AM2+AN2=MN2 ， 且AM=2a，AN=a，
∴MN= 
a．
同理可得：MC= 
a，NC=5a．
∵MN2+MC2=（ a）2+（ a）2=25a2 ， NC2=（5a）2=25a2 ，
∴MN2+MC2=NC2 ，
∴△CMN是直角三角形
【解析】可設正方形ABCD的邊長為4a，利用勾股定理分別求出NC，MN，CM的值，計算得出MN2+MC2=NC2 ， 根據勾股定理的逆定理可判定△CMN是直角三角形．
【考點精析】利用勾股定理的概念和勾股定理的逆定理對題目進行判斷即可得到答案，需要熟知直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2；如果三角形的三邊長a、b、c有下面關系：a2+b2=c2，那么這個三角形是直角三角形．
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】為了加強對校內外安全監控，創建荔灣平安校園，某學校計劃增加15臺監控攝像設備，現有甲、乙兩種型號的設備，其中每臺價格，有效監控半徑如表所示，經調查，購買1臺甲型設備比購買1臺乙型設備多150元，購買2臺甲型設備比購買3臺乙型設備少400元．
甲型 | 乙型 | |
價格（元/臺） | a | b |
有效半徑（米/臺） | 150 | 100 |
（1）求a、b的值．
（2）若購買該批設備的資金不超過11000元，且兩種型號的設備均要至少買一臺，學校有哪幾種購買方案？
（3）在（2）問的條件下，若要求監控半徑覆蓋范圍不低于1600米，為了節約資金，請你設計一種最省錢的購買方案．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點P是∠AOB的邊OB上的一點，過點P畫OB的垂線，交OA于點C；
（1）①過點C畫OB的平行線CD；②過點P畫OA的垂線，垂足為H；
（2）線段PH的長度是點P到的距離，線段的長度是點C到直線OB的距離．線段PC、PH、OC這三條線段大小關系是（用“＜”號連接）.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某市人口數為190.1萬人，用科學記數法表示該市人口數為（ ）
A.1.901×106人
B.19.01×105 人
C.190.1×104人
D.1901×103人
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在邊長為1的小正方形組成的方格紙中，若多邊形的各頂點都在方格紙的格點（橫豎格子線的交錯點）上，這樣的多邊形稱為格點多邊形．記格點多邊形內的格點數為a，邊界上的格點數為b，則格點多邊形的面積可表示為
，其中m，n為常數．
（1）在下面的方格中各畫出一個面積為6的格點多邊形，依次為三角形、平行四邊形（非菱形）、菱形；
（2）利用（1）中的格點多邊形確定m，n的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
