
【題目】某學校從甲、乙兩名班主任中選拔一名參加教育局組織的班主任技能比賽,選拔內容分案例分析、班會設計、情景問答三個項目,選拔比賽結束后,統計的這兩位班主任成績并制成了如圖所示的條形統計圖:
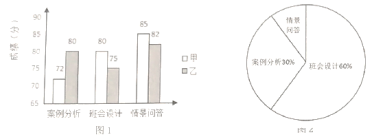
(1)乙班主任三個項目的成績中位數是______________________;
(2)用6張相同的卡片分別寫上甲、乙兩名班主任的六項成績,洗勻后,從中任意抽取一張,求抽到的卡片寫有“80”的概率;
(3)若按照圖2所示的權重比進行計算,選拔分數最高的一名班主任參加比賽,應確定哪名班主任獲得參賽資格,說明理由.
 備戰中考寒假系列答案
備戰中考寒假系列答案科目:初中數學 來源: 題型:
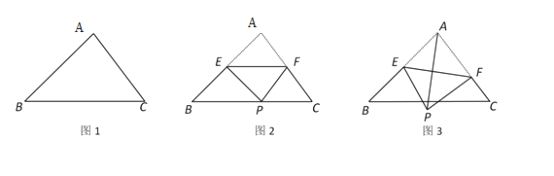
【題目】如圖,在△ABC中,AB=![]() ,∠B=45°,∠C=60°.
,∠B=45°,∠C=60°.
(1)求BC邊上的高線長.
(2)點E為線段AB的中點,點F在邊AC上,連結EF,沿EF將△AEF折疊得到△PEF.
①如圖2,當點P落在BC上時,求∠AEP的度數.
②如圖3,連結AP,當PF⊥AC時,求AP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,![]() 為原點,拋物線
為原點,拋物線![]() 經過點
經過點![]() ,對稱軸為直線
,對稱軸為直線![]() ,點
,點![]() 關于直線
關于直線![]() 的對稱點為點
的對稱點為點![]() .過點
.過點![]() 作直線
作直線![]() 軸,交
軸,交![]() 軸于點
軸于點![]() .
.
(Ⅰ)求該拋物線的解析式及對稱軸;
(Ⅱ)點![]() 在
在![]() 軸上,當
軸上,當![]() 的值最小時,求點
的值最小時,求點![]() 的坐標;
的坐標;
(Ⅲ)拋物線上是否存在點![]() ,使得
,使得![]() ,若存在,求出點
,若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=8,BC=6,D為AB邊上的動點,過點D作DE⊥AB交邊AC于點E,過點E作EF⊥DE交BC于點F,連接DF.
(1)當AD=4時,求EF的長度;
(2)求△DEF的面積的最大值;
(3)設O為DF的中點,隨著點D的運動,則點O的運動路徑的長度為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊三角形![]() 中,
中,![]() 點
點![]() 在邊
在邊![]() 上,
上,![]() .點
.點![]() 為邊
為邊![]() 上一動點(不與點
上一動點(不與點![]() 重合),連接
重合),連接![]() 關于
關于![]() 的軸對稱圖形為
的軸對稱圖形為![]() .
.
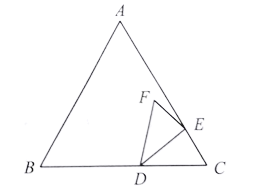
(1)當點![]() 在
在![]() 上時,求證:
上時,求證:![]() ;
;
(2)當![]() 三點共線時,求
三點共線時,求![]() 的長;
的長;
(3)連接![]() 設
設![]() 的面積為
的面積為![]() 的面積為
的面積為![]() 記
記![]()
![]() 是否存在最大值?若存在,請直接寫出
是否存在最大值?若存在,請直接寫出![]() 的最大值;若不存在,請說明理由.
的最大值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形![]() 的邊長為4,點
的邊長為4,點![]() 在對角線
在對角線![]() 上(可與點
上(可與點![]() 重合),
重合),![]() ,點
,點![]() 在正方形的邊上.下面四個結論中,
在正方形的邊上.下面四個結論中,
①存在無數個四邊形![]() 是平行四邊形;
是平行四邊形;
②存在無數個四邊形![]() 是菱形;
是菱形;
③存在無數個四邊形![]() 是矩形;
是矩形;
④至少存在一個四邊形![]() 是正方形.
是正方形.
所有正確結論的序號是_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
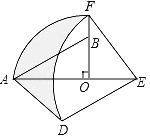
【題目】如圖,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,將Rt△AOB繞點O順時針旋轉90°后得Rt△FOE,將線段EF繞點E逆時針旋轉90°后得線段ED,分別以O,E為圓心,OA、ED長為半徑畫弧AF和弧DF,連接AD,則圖中陰影部分面積是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
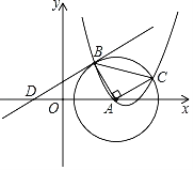
【題目】如圖,已知的圓心為點![]() ,拋物線y=ax2﹣
,拋物線y=ax2﹣![]() x+c過點A,與
x+c過點A,與![]() 交于B、C兩點,連接AB、AC,且AB⊥AC,B、C兩點的縱坐標分別是2、1.
交于B、C兩點,連接AB、AC,且AB⊥AC,B、C兩點的縱坐標分別是2、1.
(1)求B、C點坐標和拋物線的解析式;
(2)直線y=kx+1經過點B,與x軸交于點D.點E(與點D不重合)在該直線上,且AD=AE,請判斷點E是否在此拋物線上,并說明理由;
(3)如果直線y=k1x﹣1與⊙A相切,請直接寫出滿足此條件的直線解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為提高飲水質量,越來越多的居民開始選購家用凈水器.一商家抓住商機,從廠家購進了A、B兩種型號家用凈水器共160臺,A型號家用凈水器進價是150元/臺,B型號家用凈水器進價是350元/臺,購進兩種型號的家用凈水器共用去36000元.
(1)求A、B兩種型號家用凈水器各購進了多少臺;
(2)為使每臺B型號家用凈水器的毛利潤是A型號的2倍,且保證售完這160臺家用凈水器的毛利潤不低于11000元,求每臺A型號家用凈水器的售價至少是多少元?(注:毛利潤=售價﹣進價)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com