
 x+
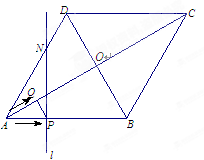
x+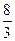 與直線l2:y=2x+16相交于點C,l1,l2分別交x軸于A,B兩點.矩形DEFG的頂點D,E分別在直線l1,l2上,頂點F,G都在X軸上,且點G與點B重合.
與直線l2:y=2x+16相交于點C,l1,l2分別交x軸于A,B兩點.矩形DEFG的頂點D,E分別在直線l1,l2上,頂點F,G都在X軸上,且點G與點B重合.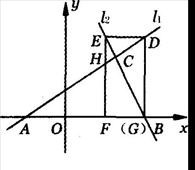
 x+
x+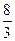 =0,得x=-4.
=0,得x=-4.
 y=
y= x=5
x=5 AB·yc=
AB·yc= ×12×6=36. ……4分
×12×6=36. ……4分 ×8+
×8+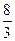 =8.
=8.
 ,即
,即 .∴RG=2t.
.∴RG=2t. (8-t).
(8-t). ×t×2t-
×t×2t- (8-t)×
(8-t)× (8-t).
(8-t). t2+
t2+ t+
t+ . ……l0分
. ……l0分 (8-t),∵Rt△AGR∽Rt△AMC,∴
(8-t),∵Rt△AGR∽Rt△AMC,∴ .
. ,∴RG=
,∴RG= (12-t).
(12-t). (HF+RG)×FG=
(HF+RG)×FG= [
[ (8-t)+
(8-t)+  (12-t)] ×4=-
(12-t)] ×4=- t+
t+ . ……12分
. ……12分 (12-t).
(12-t). AG×RG=
AG×RG= (12-t)×
(12-t)× (12-t)=
(12-t)= (12-t) 2=
(12-t) 2= t 2-8t+
t 2-8t+ . ……l4分
. ……l4分

科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
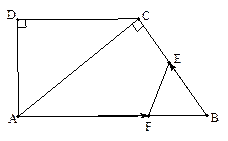
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 ,這個矩形的長寬各是多少?
,這個矩形的長寬各是多少?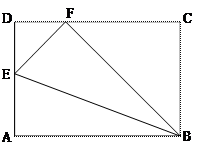
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
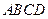 中,
中,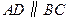 ,
,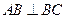 ,以
,以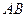 為直徑的
為直徑的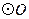 與
與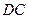 相切于
相切于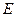 .已知
.已知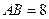 ,邊
,邊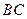 比
比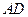 大6.
大6.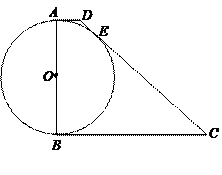
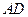 、
、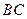 的長.
的長.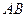 上是否存在一動點
上是否存在一動點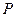 ,使以
,使以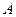 、
、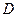 、
、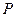 為頂點的三角形與
為頂點的三角形與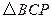 相似?若存在,求出
相似?若存在,求出 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 中,D是AC上一點,聯結BD,且∠ABD =∠ACB.
中,D是AC上一點,聯結BD,且∠ABD =∠ACB.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com