
【題目】如圖,在ABCD中,F是AD的中點,延長BC到點E,使CE=![]() BC,連接DE,CF.
BC,連接DE,CF.
(1)求證:四邊形CEDF是平行四邊形;
(2)若AB=4,AD=6,∠B=60°,求DE的長.

【答案】(1)見解析;(2)![]()
【解析】試題分析:(1)由“平行四邊形的對邊平行且相等”的性質推知AD∥BC,且AD=BC;然后根據中點的定義、結合已知條件推知四邊形CEDF的對邊平行且相等(DF=CE,且DF∥CE),即四邊形CEDF是平行四邊形;
(2)如圖,過點D作DH⊥BE于點H,構造含30度角的直角△DCH和直角△DHE.通過解直角△DCH和在直角△DHE中運用勾股定理來求線段ED的長度.
試題解析:(1)證明:在ABCD中,AD∥BC,且AD=BC.
∵F是AD的中點,
∴DF=![]() AD.
AD.
又∵CE=![]() BC,
BC,
∴DF=CE,且DF∥CE,
∴四邊形CEDF是平行四邊形;
如圖,過點D作DH⊥BE于點H.

在ABCD中,∵∠B=60°,
∴∠DCE=60°.
∵AB=4,
∴CD=AB=4,
∴CH=![]() CD=2,DH=2
CD=2,DH=2![]() .
.
在CEDF中,CE=DF=![]() AD=3,則EH=1.
AD=3,則EH=1.
∴在Rt△DHE中,根據勾股定理知DE=![]() .
.


 全優沖刺100分系列答案
全優沖刺100分系列答案 英才點津系列答案
英才點津系列答案科目:初中數學 來源: 題型:
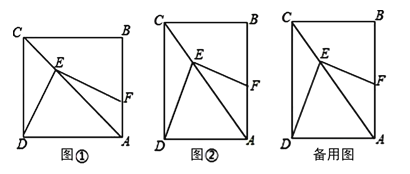
【題目】(本題滿分9分)小明一直對四邊形很感興趣,在矩形ABCD中,E是AC上任意一點,連接DE,作DE⊥EF,交AB于點F.請你跟著他一起解決下列問題:
(1)如圖①,若AB=BC,則DE,EF有什么數量關系?請給出證明.
(2)如圖②,若∠CAB=30°,則DE,EF又有什么數量關系?請給出證明.
(3)由(1)、(2)這兩種特殊情況,小明提出問題:如果在矩形ABCD中,BC=mAB,那DE,EF有什么數量關系?請給出證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊△OAB和等邊△AFE的一邊都在x軸上,雙曲線y=![]() (k>0)經過邊OB的中點C和AE的中點D.已知等邊△OAB的邊長為4.
(k>0)經過邊OB的中點C和AE的中點D.已知等邊△OAB的邊長為4.
(1)求該雙曲線所表示的函數解析式;
(2)求等邊△AEF的邊長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】交通安全是社會關注的熱點問題,安全隱患主要是超速和超載.某中學八年級數學活動小組的同學進行了測試汽車速度的實驗.如圖,先在筆直的公路1旁選取一點P,在公路1上確定點O、B,使得PO⊥l,PO=100米,∠PBO=45°.這時,一輛轎車在公路1上由B向A勻速駛來,測得此車從B處行駛到A處所用的時間為3秒,并測得∠APO=60°.此路段限速每小時80千米,試判斷此車是否超速?請說明理由(參考數據: ![]() =1.41,
=1.41, ![]() =1.73).
=1.73). 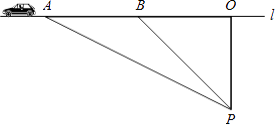
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com