
【題目】周末,小明從家步行去書店看書.出發![]() 小時后距家1.8千米時,爸爸駕車從家沿相同路線追趕小明,在
小時后距家1.8千米時,爸爸駕車從家沿相同路線追趕小明,在![]() 地追上小明后,二人駕車繼續前行到達書店.小明在書店
地追上小明后,二人駕車繼續前行到達書店.小明在書店![]() 看書,爸爸去單位
看書,爸爸去單位![]() 地辦事.如圖是小明與爸爸兩人之間距離
地辦事.如圖是小明與爸爸兩人之間距離![]() (千米)與小明出發的時間
(千米)與小明出發的時間![]() (小時)之間的函數圖象,(小明步行速度與爸爸駕車速度始終保持不變,彼此交流時間忽略不計),請根據圖象回答下列問題:
(小時)之間的函數圖象,(小明步行速度與爸爸駕車速度始終保持不變,彼此交流時間忽略不計),請根據圖象回答下列問題:
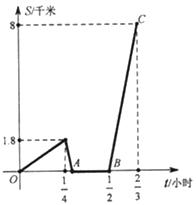
(1)小明步行速度是_____千米/小時,爸爸駕車速度是______千米/小時:
(2)圖中點![]() 的坐標是______:
的坐標是______:
(3)求書店與家的路程;
(4)求爸爸出發多長時間,兩人相距3千米.
【答案】(1)7.2,48;(2)![]() ;(3)12千米;(4)爸爸出發
;(3)12千米;(4)爸爸出發![]() 小時后,兩人相距3千米
小時后,兩人相距3千米
【解析】
(1)根據速度=距離÷時間即可求出小明和爸爸的速度;(2)設t小時爸爸追上小明,根據追上時距離相等列方程求出t值,進而可求出A點坐標;(3)根據爸爸出發到書店所用時間為(![]() )小時,乘以爸爸的速度即可得答案;(4)由圖象可知兩人相距3千米時在圖象線段BC上,設直線BC的解析式為S=kt+b,根據B、C兩點坐標,利用待定系數法求出k、b的值,即可得BC的解析式,把S=3代入求出t的值,根據爸爸出發的時間等于t-
)小時,乘以爸爸的速度即可得答案;(4)由圖象可知兩人相距3千米時在圖象線段BC上,設直線BC的解析式為S=kt+b,根據B、C兩點坐標,利用待定系數法求出k、b的值,即可得BC的解析式,把S=3代入求出t的值,根據爸爸出發的時間等于t-![]() 即可得答案.
即可得答案.
(1)小明步行速度為:1.8÷![]() =7.2(千米/小時),
=7.2(千米/小時),
爸爸駕車速度為:8÷(![]() )=48(千米/小時),
)=48(千米/小時),
故答案為:7.2,48
(2)設t小時爸爸追上小明,
∴48t=7.2t+1.8,
解得:t=![]() ,
,
∴tA=![]() +
+![]() =
=![]() ,
,
∴A點坐標為(![]() ,0),
,0),
故答案為:(![]() ,0)
,0)
(3)爸爸出發到書店所用時間為(![]() )小時,
)小時,
∴書店與家的路程為:48×(![]() )=12(千米),
)=12(千米),
答:書店與家的路程為12千米.
(4)由圖象可知兩人相距3千米時在圖象線段BC上,設直線BC的解析式為S=kt+b,
∵B(![]() ,0),C(
,0),C(![]() ,8),
,8),
∴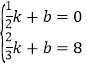 ,
,
解得:![]() ,
,
∴BC的解析式為S=48t-24,
當S=3時,3=48t-24,
解得:t=![]() ,
,
∵爸爸從![]() 小時出發,
小時出發,
∴![]() -
-![]() =
=![]() (小時),
(小時),
答:爸爸出發![]() 小時,兩人相距3千米.
小時,兩人相距3千米.


科目:初中數學 來源: 題型:
【題目】對于二次函數y=x2+mx+1,當0<x≤2時的函數值總是非負數,則實數m的取值范圍為( )
A. m≥﹣2 B. ﹣4≤m≤﹣2 C. m≥﹣4 D. m≤﹣4或m≥﹣2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,點M在x軸上,以點M為圓心,2.5長為半徑的圓交y軸于A、B兩點,交x軸于C(x1,0)、D(x2,0)兩點,(x1<x2),x1、x2是方程x(2x+1)=(x+2)2的兩根.
(1)求點C、D及點M的坐標;
(2)若直線y=kx+b切⊙M于點A,交x軸于P,求PA的長;
(3)⊙M上是否存在這樣的點Q,使點Q、A、C三點構成的三角形與△AOC相似?若存在,請求出點的坐標,并求出過A、C、Q三點的拋物線的解析式;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是半圓O的直徑,點C在半圓外,AC,BC與半圓交于D點和E點.
(1)請只用無刻度的直尺作出△ABC的兩條高線,并寫出作法;
(2)若AC=AB,連接DE,BE,求證:DE=BE.

查看答案和解析>>
科目:初中數學 來源: 題型:
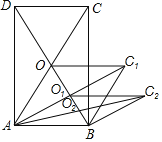
【題目】如圖,矩形ABCD的面積為20cm2,對角線交于點O,以AB、AO為鄰邊作平行四邊形AOC1B,對角線交于點O1;以AB、AO1為鄰邊作平行四邊形AO1C2B2;…;依此類推,則平行四邊形AO4C5B的面積為________,平行四邊形AOnCn+1B的面積為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據解答過程填空(寫出推理理由或根據):
如圖,已知∠DAF=∠F,∠B=∠D,試說明AB//DC

證明∵∠DAF=∠F( 已知)
∴AD∥BF ( )
∴∠D=∠DCF( )
∵∠B=∠D( )
∴∠ =∠DCF(等量代換)
∴AB//DC( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=x2+bx+c(b、c是常數)與x軸有兩個交點,其中有一點的坐標為A(1,0),點P(m,t)(m≠0)為拋物線上的一個動點.
(1)設y′=m+t,寫出y′關于m的函數解析式,并求出該函數圖象的對稱軸(用含c的代數式表示);
(2)在(1)的條件下,當m≤3時,與其對應的函數y′的最小值為﹣![]() ,求拋物線y=x2+bx+c的解析式;
,求拋物線y=x2+bx+c的解析式;
(3)在(2)的條件下,P點關于原點的對稱點為P′,且P′落在第一象限內,當P′A2取得最小值時,求m與t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖 1,C為線段 AB上一點,以 AC,BC為一邊,在 AB同側做長方形 ACDE和長方形 CBFG,且 滿足 AC=2AE,CB=2BF,記 AC2a,BC2b(a b) .
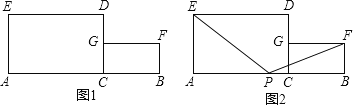
(1)記長方形 ACDE的面積為 s1 ,長方形 CBFG的面積為 s2 .若 AB6, a2b ,求 s1 s2 .
(2)如圖 2,點 P是線段 CA上的動點.
①當點 P從點 C向左移動![]() 個單位后,求△EAP與△FBP的面積之差.
個單位后,求△EAP與△FBP的面積之差.
②當點 P從點 C向左移動 ![]() 個單位后,△EAP與△FBP的面積之差記為 m1 ; 當點 P從點 C向左移動 (a b) 個單位后,△EAP與△FBP的面積之差記為 m2 ,求
個單位后,△EAP與△FBP的面積之差記為 m1 ; 當點 P從點 C向左移動 (a b) 個單位后,△EAP與△FBP的面積之差記為 m2 ,求 ![]() 的值(結果用含 n 的代數式表示).
的值(結果用含 n 的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市推出電腦上網包月制,每月收取費用y(元)與上網時間x(小時)的函數關系如圖所示,其中BA是線段,且BA∥x軸,AC是射線.
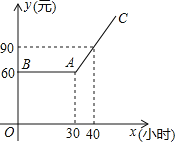
(1)若小李11月份上網20小時,他應付多少元的上網費用?
(2)當x≥30,求y與x之間的函數關系式;
(3)若小李12月份上網費用為135元,則他在該月份的上網時間是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com