
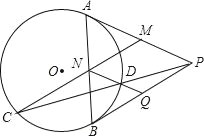
【題目】如圖所示,PA、PB為⊙O的切線,M、N是PA、AB的中點,連接MN交⊙O點C,連接PC交⊙O于D,連接ND交PB于Q,求證:MNQP為菱形.
【答案】見解析
【解析】試題分析:連接OA,OB,OC,OD,OP. 由![]() 是
是![]() 的中點,根據三角形中位線的性質,可得MN∥BP.,又由PA、PB為
的中點,根據三角形中位線的性質,可得MN∥BP.,又由PA、PB為![]() 的切線,可得AB⊥OP.可證得NM=MP,然后由射影定理與切割線定理證得O,C,D,N四點共圓,繼而證得
的切線,可得AB⊥OP.可證得NM=MP,然后由射影定理與切割線定理證得O,C,D,N四點共圓,繼而證得
MP∥NQ,則可得四邊形MNQP是平行四邊形,證得四邊形MNQP是菱形.
試題解析:證明:連接OA,OB,OC,OD,OP.
∵AN=NB,AM=MP.
∴MN∥BP.
∵PA、PB為![]() 的切線,
的切線,
∴AB⊥OP.
∴NM=MP,∠MNP=∠MPN,
在Rt△AOP中,由射影定理,得![]()
由切割線定理,得![]()
∴PNPO=PDPC,
∴O,C,D,N四點共圓,
∴∠PND=∠OCD,∠ONC=∠ODC,
∵OC=OD,
∴∠OCD=∠ODC,
∵∠MNP=∠ONC,
∴∠MNP=∠PND=∠MPN,
∴MP∥NQ,
∴四邊形MNQP是平行四邊形,
∴四邊形MNQP是菱形.


 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:初中數學 來源: 題型:
【題目】 觀察下列三行數:
2,4,8,16,32,![]()
![]() ,1,2,4,8,
,1,2,4,8,![]()
1,5,7,17,31,![]()
如圖,第一行數的第n(n為正整數)個數![]() 用來表示,第二行數的第n個數用
用來表示,第二行數的第n個數用![]() 來表示,第三行數的第n個數用
來表示,第三行數的第n個數用![]() 來表示
來表示
(1)根據你發現的規律,請用含n的代數式表示數![]() ,
,![]() ,
,![]() 的值
的值![]() = ;
= ; ![]() = ;
= ; ![]() = ;
= ;
(2)取每行的第6個數,計算這三個數的和
(3)若![]() 記為x,求
記為x,求![]() (結果用含x的式子表示并化簡)
(結果用含x的式子表示并化簡)
查看答案和解析>>
科目:初中數學 來源: 題型:
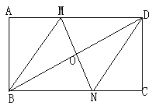
【題目】如圖,在矩形ABCD中,對角線BD的垂直平分線MN與AD相交于點N,連接BM,DN.
(1)求證:四邊形BMDN是菱形;
(2)若AB=4,AD=8,求MD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
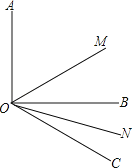
(1)求∠MON的度數;
(2)如果∠AOB=α,其他條件不變,求∠MON的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
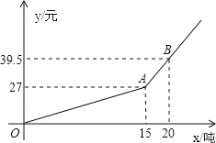
【題目】某市自來水公司為鼓勵居民節約用水,采取按月用水量分段收費辦法,若某戶居民應交交費![]() (元)與用水量
(元)與用水量![]() (噸)的函數關系如圖所示。
(噸)的函數關系如圖所示。
(1)分別寫出當![]() 和
和![]() 時,
時,![]() 與
與![]() 的函數關系式;
的函數關系式;
(2)若某用戶該月用水21噸,則應交水費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
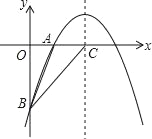
【題目】如圖,二次函數y=﹣![]() x2+bx+c的圖象經過A(2,0),B(0,﹣6)兩點,
x2+bx+c的圖象經過A(2,0),B(0,﹣6)兩點,
(1)求這個二次函數的解析式;
(2)設該二次函數的對稱軸與x軸交于點C,連接BA,BC,求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,G為BC邊上一點,BE⊥AG于E,DF⊥AG于F,連接DE.
(1)求證:△ABE≌△DAF;
(2)若AF=1,四邊形ABED的面積為6,求EF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在三角形![]() 中,
中,![]() .將三角形
.將三角形![]() 繞著點
繞著點![]() 旋轉,使得點
旋轉,使得點![]() 落在直線
落在直線![]() 上的點
上的點![]() ,點
,點![]() 落在點
落在點![]() .
.
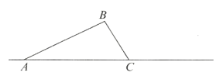
(1)畫出旋轉后的三角形![]() .
.
(2)求線段![]() 在旋轉的過程中所掃過的面積(保留
在旋轉的過程中所掃過的面積(保留![]() ).
).
(3)如果在三角形![]() 中,
中,![]() (其中
(其中![]() ).其他條件不變,請你用含有
).其他條件不變,請你用含有![]() 的代數式,直接寫出線段
的代數式,直接寫出線段![]() 旋轉的過程中所掃過的面積(保留
旋轉的過程中所掃過的面積(保留![]() ).
).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com