
【題目】如圖,信號塔PQ座落在坡度i=1:2的山坡上,其正前方直立著一警示牌.當太陽光線與水平線成60°角時,測得信號塔PQ落在斜坡上的影子QN長為2 ![]() 米,落在警示牌上的影子MN長為3米,求信號塔PQ的高.(結果不取近似值)
米,落在警示牌上的影子MN長為3米,求信號塔PQ的高.(結果不取近似值)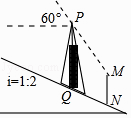
【答案】解:如圖作MF⊥PQ于F,QE⊥MN于E,則四邊形EMFQ是矩形.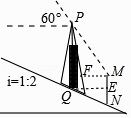
在Rt△QEN中,設EN=x,則EQ=2x,
∵QN2=EN2+QE2 ,
∴20=5x2 ,
∵x>0,
∴x=2,
∴EN=2,EQ=MF=4,
∵MN=3,
∴FQ=EM=1,
在Rt△PFM中,PF=FMtan60°=4 ![]() ,
,
∴PQ=PF+FQ=4 ![]() +1
+1
【解析】如圖作MF⊥PQ于F,QE⊥MN于E,則四邊形EMFQ是矩形.分別在Rt△EQN、Rt△PFM中解直角三角形即可解決問題.
【考點精析】解答此題的關鍵在于理解勾股定理的概念的相關知識,掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2,以及對關于坡度坡角問題的理解,了解坡面的鉛直高度h和水平寬度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面與水平面的夾角記作A(叫做坡角),那么i=h/l=tanA.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2+(2m+1)x+m2﹣4=0
(1)當m為何值時,方程有兩個不相等的實數根?
(2)若邊長為5的菱形的兩條對角線的長分別為方程兩根的2倍,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在面積都相等的所有矩形中,當其中一個矩形的一邊長為1時,它的另一邊長為3.
(1)設矩形的相鄰兩邊長分別為x,y.
①求y關于x的函數表達式;
②當y≥3時,求x的取值范圍;
(2)圓圓說其中有一個矩形的周長為6,方方說有一個矩形的周長為10,你認為圓圓和方方的說法對嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,E是BC上一點,連接AE,將矩形沿AE翻折,使點B落在CD邊F處,連接AF,在AF上取點O,以O為圓心,OF長為半徑作⊙O與AD相切于點P.若AB=6,BC=3 ![]() ,則下列結論:①F是CD的中點;②⊙O的半徑是2;③AE=
,則下列結論:①F是CD的中點;②⊙O的半徑是2;③AE= ![]() CE;④S陰影=
CE;④S陰影= ![]() .其中正確結論的序號是 .
.其中正確結論的序號是 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一副三角尺按如圖的位置擺放(頂點C 與F 重合,邊CA與邊FE疊合,頂點B、C、D在一條直線上).將三角尺DEF繞著點F按順時針方向旋轉n°后(0<n<180 ),如果EF∥AB,那么n的值是 . 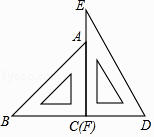
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在平面直角坐標系xOy中(如圖),已知拋物線y=﹣x2+bx+c經過點A(2,2),對稱軸是直線x=1,頂點為B.
(1)求這條拋物線的表達式和點B的坐標;
(2)點M在對稱軸上,且位于頂點上方,設它的縱坐標為m,聯結AM,用含m的代數式表示∠AMB的余切值;
(3)將該拋物線向上或向下平移,使得新拋物線的頂點C在x軸上.原拋物線上一點P平移后的對應點為點Q,如果OP=OQ,求點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小華和小軍做摸球游戲:A袋裝有編號為1,2,3的三個小球,B袋裝有編號為4,5,6的三個小球,兩袋中的所有小球除編號外都相同.從兩個袋子中分別隨機摸出一個小球,若B袋摸出小球的編號與A袋摸出小球的編號之差為偶數,則小華勝,否則小軍勝,這個游戲對雙方公平嗎?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com