
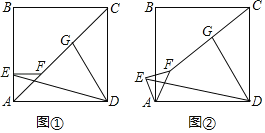
【題目】如圖,四邊形ABCD為正方形,△AEF為等腰直角三角形,∠AEF=90°,連接FC,G為FC的中點,連接GD,ED.
(1)如圖①,E在AB上,直接寫出ED,GD的數量關系.
(2)將圖①中的△AEF繞點A逆時針旋轉,其它條件不變,如圖②,(1)中的結論是否成立?說明理由.
(3)若AB=5,AE=1,將圖①中的△AEF繞點A逆時針旋轉一周,當E,F,C三點共線時,直接寫出ED的長.
【答案】(1)DE=![]() DG;(2)成立,理由見解析;(3)DE的長為4
DG;(2)成立,理由見解析;(3)DE的長為4![]() 或3
或3![]() .
.
【解析】
(1)根據題意結論:DE=![]() DG,如圖1中,連接EG,延長EG交BC的延長線于M,連接DM,證明△CMG≌△FEG(AAS),推出EF=CM,GM=GE,再證明△DCM≌△DAE(SAS)即可解決問題;
DG,如圖1中,連接EG,延長EG交BC的延長線于M,連接DM,證明△CMG≌△FEG(AAS),推出EF=CM,GM=GE,再證明△DCM≌△DAE(SAS)即可解決問題;
(2)如圖2中,結論成立.連接EG,延長EG到M,使得GM=GE,連接CM,DM,延長EF交CD于R,其證明方法類似;
(3)由題意分兩種情形:①如圖3-1中,當E,F,C共線時.②如圖3-3中,當E,F,C共線時,分別求解即可.
解:(1)結論:DE=![]() DG.
DG.
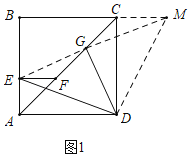
理由:如圖1中,連接EG,延長EG交BC的延長線于M,連接DM.
∵四邊形ABCD是正方形,
∴AD=CD,∠B=∠ADC=∠DAE=∠DCB=∠DCM=90°,
∵∠AEF=∠B=90°,
∴EF∥CM,
∴∠CMG=∠FEG,
∵∠CGM=∠EGF,GC=GF,
∴△CMG≌△FEG(AAS),
∴EF=CM,GM=GE,
∵AE=EF,
∴AE=CM,
∴△DCM≌△DAE(SAS),
∴DE=DM,∠ADE=∠CDM,
∴∠EDM=∠ADC=90°,
∴DG⊥EM,DG=GE=GM,
∴△EGD是等腰直角三角形,
∴DE=![]() DG.
DG.
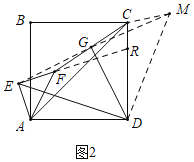
(2)如圖2中,結論成立.
理由:連接EG,延長EG到M,使得GM=GE,連接CM,DM,延長EF交CD于R.
∵EG=GM,FG=GC,∠EGF=∠CGM,
∴△CGM≌△FGE(SAS),
∴CM=EF,∠CMG=∠GEF,
∴CM∥ER,
∴∠DCM=∠ERC,
∵∠AER+∠ADR=180°,
∴∠EAD+∠ERD=180°,
∵∠ERD+∠ERC=180°,
∴∠DCM=∠EAD,
∵AE=EF,
∴AE=CM,
∴△DAE≌△DCM(SAS),
∴DE=DM,∠ADE=∠CDM,
∴∠EDM=∠ADC=90°,
∵EG=GM,
∴DG=EG=GM,
∴△EDG是等腰直角三角形,
∴DE=![]() DG.
DG.
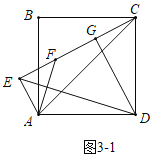
(3)①如圖3﹣1中,當E,F,C共線時,
在Rt△ADC中,AC=![]() =
=![]() =5
=5![]() ,
,
在Rt△AEC中,EC=![]() =
=![]() =7,
=7,
∴CF=CE﹣EF=6,
∴CG=![]() CF=3,
CF=3,
∵∠DGC=90°,
∴DG=![]() =
=![]() =4,
=4,
∴DE=![]() DG=4
DG=4![]() .
.
②如圖3﹣3中,當E,F,C共線時,同法可得DE=3![]() .
.
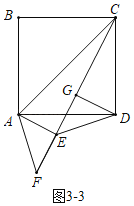
綜上所述,DE的長為4![]() 或3
或3![]() .
.


 名師金手指領銜課時系列答案
名師金手指領銜課時系列答案科目:初中數學 來源: 題型:
【題目】某數學社團成員想利用所學的知識測量某廣告牌的寬度![]() 圖中線段MN的長
圖中線段MN的長![]() ,直線MN垂直于地面,垂足為點
,直線MN垂直于地面,垂足為點![]() 在地面A處測得點M的仰角為
在地面A處測得點M的仰角為![]() 、點N的仰角為
、點N的仰角為![]() ,在B處測得點M的仰角為
,在B處測得點M的仰角為![]() ,
,![]() 米,且A、B、P三點在一直線上
米,且A、B、P三點在一直線上![]() 請根據以上數據求廣告牌的寬MN的長.
請根據以上數據求廣告牌的寬MN的長.
![]() 參考數據:
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分線分別交AB、AC于點D、E,則以下AE與CE的數量關系正確的是( )

A.AE=![]() CEB.AE=
CEB.AE=![]() CEC.AE=
CEC.AE=![]() CED.AE=2CE
CED.AE=2CE
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 “低碳生活,綠色出行”的理念正逐漸被人們所接受,越來越多的人選擇騎自行車上下班.王叔叔某天騎自行車上班從家出發到單位過程中行進速度v(米/分鐘)隨時間t(分鐘)變化的函數圖象大致如圖所示,圖象由三條線段OA、AB和BC組成.設線段OC上有一動點T(t,0),直線l左側部分的面積即為t分鐘內王叔叔行進的路程s(米).
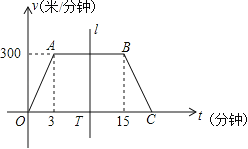
(1)①當t=2分鐘時,速度v= 米/分鐘,路程s= 米;
②當t=15分鐘時,速度v= 米/分鐘,路程s= 米.
(2)當0≤t≤3和3<t≤15時,分別求出路程s(米)關于時間t(分鐘)的函數解析式;
(3)求王叔叔該天上班從家出發行進了750米時所用的時間t.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】國家教育部提出“每天鍛煉一小時,健康工作五十年,幸福生活一輩子”.萬州區某中學對九年級部分學生進行問卷調查“你最喜歡的鍛煉項目是什么?”,規定從“打球”,“跑步”,“游泳”,“跳繩”,“其他”五個選項中選擇自己最喜歡的項目,且只能選擇一個項目,并將調查結果繪制成如下兩幅不完整的統計圖.
最喜歡的鍛煉項目 | 人數 |
打球 | 120 |
跑步 |
|
游泳 |
|
跳繩 | 30 |
其他 |
|
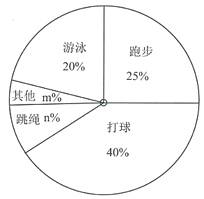
(1)這次問卷調查的學生總人數為 ,人數![]() ;
;
(2)扇形統計圖中,![]() ,“其他”對應的扇形的圓心角的度數為 度;
,“其他”對應的扇形的圓心角的度數為 度;
(3)若該年級有1200名學生,估計喜歡“跳繩”項目的學生大約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為積極參與鄂州市全國文明城市創建活動,我市某校在教學樓頂部新建了一塊大型宣傳牌,如下圖.小明同學為測量宣傳牌的高度![]() ,他站在距離教學樓底部
,他站在距離教學樓底部![]() 處6米遠的地面
處6米遠的地面![]() 處,測得宣傳牌的底部
處,測得宣傳牌的底部![]() 的仰角為
的仰角為![]() ,同時測得教學樓窗戶
,同時測得教學樓窗戶![]() 處的仰角為
處的仰角為![]() (
(![]() 、
、![]() 、
、![]() 、
、![]() 在同一直線上).然后,小明沿坡度
在同一直線上).然后,小明沿坡度![]() 的斜坡從
的斜坡從![]() 走到
走到![]() 處,此時
處,此時![]() 正好與地面
正好與地面![]() 平行.
平行.
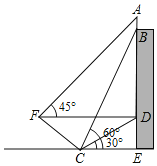
(1)求點![]() 到直線
到直線![]() 的距離(結果保留根號);
的距離(結果保留根號);
(2)若小明在![]() 處又測得宣傳牌頂部
處又測得宣傳牌頂部![]() 的仰角為
的仰角為![]() ,求宣傳牌的高度
,求宣傳牌的高度![]() (結果精確到0.1米,
(結果精確到0.1米,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有下列說法:①為預防新型冠狀病毒肺炎,學校檢查師生佩戴口罩的情況,應采用全面調查;②從![]() 名學生中選出
名學生中選出![]() 名學生進行抽樣調查,樣本容量為
名學生進行抽樣調查,樣本容量為![]() ;③“任意買一張電影票座位號是奇數”這個事件是必然事件;④數據
;③“任意買一張電影票座位號是奇數”這個事件是必然事件;④數據![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的方差是
的方差是![]() .其中說法正確的有( )
.其中說法正確的有( )
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,A(-4,3),B(0,1),將線段AB沿
中,A(-4,3),B(0,1),將線段AB沿![]() 軸的正方向平移
軸的正方向平移![]() 個單位,得到線段A′B′,且A′,B′恰好都落在反比例函數
個單位,得到線段A′B′,且A′,B′恰好都落在反比例函數![]() 的圖象上.
的圖象上.
(1)用含![]() 的代數式表示點A′,B′的坐標;
的代數式表示點A′,B′的坐標;
(2)求![]() 的值和反比例函數
的值和反比例函數![]() 的表達式;
的表達式;
(3)點![]() 為反比例函數
為反比例函數![]() 圖象上的一個動點,直線
圖象上的一個動點,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,若
,若![]() ,請直接寫出點C的坐標.
,請直接寫出點C的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】實行垃圾資源化利用,是社會文明水平的一個重要體現.某環保公司研發的甲、乙兩種智能設備可利用最新技術將干垃圾變身為燃料棒.某垃圾處理廠從環保公司購入以上兩種智能設備,若干已知購買甲型智能設備花費360萬元,購買乙型智能設備花費480萬元,購買的兩種設備數量相同,且兩種智能設備的單價和為140萬元.
(1)求甲乙兩種智能設備單價;
(2)垃圾處理廠利用智能設備生產燃料棒,并將產品出售.已知燃料棒的成本由人力成本和物資成本兩部分組成,其中物資成本占總成本的40%,且生產每噸燃料棒所需人力成本比物資成本的![]() 倍還多10元,調查發現:若燃料棒售價為每噸200元,平均每天可售出350噸,而當銷售價每降低1元,平均每天可多售出5噸,但售價在每噸200元基礎上降價幅度不超過7%,
倍還多10元,調查發現:若燃料棒售價為每噸200元,平均每天可售出350噸,而當銷售價每降低1元,平均每天可多售出5噸,但售價在每噸200元基礎上降價幅度不超過7%,
①垃圾處理廠想使這種燃料棒的銷售利潤平均每天達到36080元,求每噸燃料棒售價應為多少元?
②每噸燃料棒售價應為多少元時,這種燃料棒平均每天的銷售利潤最大?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com