
【題目】如圖,已知在 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,點
,點 ![]() 是
是 ![]() 的重心,則點
的重心,則點 ![]() 到
到 ![]() 所在直線的距離等于( )
所在直線的距離等于( )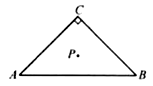
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:如圖,連接CP并延長交AB于D,連接BP交AC于E,并延長到F,使EF=PE,
∵∠C=90°,AC=BC,AB=6,
∴AC=BC=3![]() ,
,
又∵P為△ABC的重心,
∴CD=![]() AB=3.∠CDB=90°
AB=3.∠CDB=90°
在△AEF和△CEP中,
∵
∴△AEF≌△CEP.
∴∠FAD=90°,CP=AF=3-DP.
又∵CD‖FA,
∴△BPD∽△BFA.
∴![]() =
=![]() .
.
∴![]() =
=![]() .
.
∴PD=1.
所以答案是A.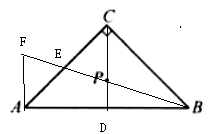
【分 析】如圖,根據三角形的重心是三條中線的交點,根據等腰直角三角形可知CD=3,可連接CP并延長交AB于D,則∠FAD=90°,連接BP交AC于E, 并延長到F,使EF=PE,然后可知△A,可得EF≌△CEP,∠FAD=90°,CP=AF=3-DP,因此可根據兩角對應相等的兩三角形相似,可得 △BPD∽△BFA.即可求出PD.
【考點精析】掌握等腰直角三角形和相似三角形的判定與性質是解答本題的根本,需要知道等腰直角三角形是兩條直角邊相等的直角三角形;等腰直角三角形的兩個底角相等且等于45°;相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方.


 考前必練系列答案
考前必練系列答案科目:初中數學 來源: 題型:
【題目】計算機系統對文件的管理通常采用樹形目錄結構,方式如圖,在一個根目錄下建立若干子目錄(這里稱第一層目錄),每個子目錄又可作為父目錄,向下繼續建立其子目錄(這里稱第二層目錄),依次進行,可創建多層目錄.現在一根目錄下建立了四層目錄,并且每一個父目錄下的子目錄的個數都相同,都等于根目錄下目錄的個數.已知第三層目錄共有343個,求這一根目錄下的所有目錄的個數.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,BD,CE分別是∠ABC,∠ACB平分線,BD,CE相交于點P.
(1)如圖1,如果∠A=60°,∠ACB=90°,則∠BPC= ;
(2)如圖2,如果∠A=60°,∠ACB不是直角,請問在(1)中所得的結論是否仍然成立?若成立,請證明:若不成立,請說明理由.
(3)小月同學在完成(2)之后,發現CD、BE、BC三者之間存在著一定的數量關系,于是她在邊CB上截取了CF=CD,連接PF,可證△CDP≌△CFP,請你寫出小月同學發現,并完成她的說理過程.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在每個小正方形的邊長為 ![]() 的網格圖形中,每個小正方形的頂點稱為格點.從一個格點移動到與之相距
的網格圖形中,每個小正方形的頂點稱為格點.從一個格點移動到與之相距 ![]() 的另一個格點的運動稱為一次跳馬變換.例如,在
的另一個格點的運動稱為一次跳馬變換.例如,在 ![]() 的正方形網格圖形中(如圖1),從點
的正方形網格圖形中(如圖1),從點 ![]() 經過一次跳馬變換可以到達點
經過一次跳馬變換可以到達點 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 等處.現有
等處.現有 ![]() 的正方形網格圖形(如圖2),則從該正方形的頂點
的正方形網格圖形(如圖2),則從該正方形的頂點 ![]() 經過跳馬變換到達與其相對的頂點
經過跳馬變換到達與其相對的頂點 ![]() ,最少需要跳馬變換的次數是( )
,最少需要跳馬變換的次數是( )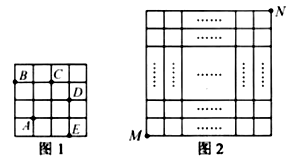
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知MB=ND,∠MBA=∠NDC,下列條件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據圖形填空:

(1)若直線ED,BC被直線AB所截,則∠1和__________是同位角.
(2)若直線ED,BC被直線AF所截,則∠3和__________是內錯角.
(3)∠1和∠3是直線AB,AF被直線__________所截構成的__________角.
(4)∠2和∠4是直線__________,__________被直線BC所截構成的__________角.
查看答案和解析>>
科目:初中數學 來源: 題型:
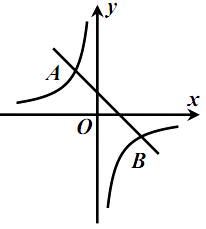
【題目】如圖,一次函數 ![]() (
( ![]() )與反比例函數
)與反比例函數 ![]() (
( ![]() )的圖象交于點
)的圖象交于點 ![]() ,
, ![]() .
.
(1)求這兩個函數的表達式;
(2)在 ![]() 軸上是否存在點
軸上是否存在點 ![]()
![]() ,使
,使 ![]() 為等腰三角形?若存在,求
為等腰三角形?若存在,求 ![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com