
【題目】“中華紫薇園”景區今年“五一”期間開始營業,為方便游客在園區內游玩休息,決定向一家園藝公司采購一批戶外休閑椅,經了解,公司出售兩種型號休閑椅,如下表:
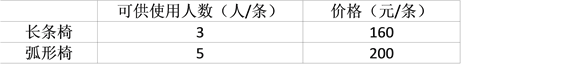
景區采購這批休閑椅共用去56000元,購得的椅子正好可讓1300名游客同時使用.
(1)求景區采購了多少條長條椅,多少條弧形椅?
(2)景區現計劃租用A、B兩種型號的卡車共20輛將這批椅子運回景區,已知A型卡車每輛可同時裝運4條長條椅和11條弧形椅,B型卡車每輛可同時裝運12條長條椅和7條弧形椅.如何安排A、B兩種卡車可一次性將這批休閑椅運回來?
(3)又知A型卡車每輛的運費為1200元,B型卡車每輛的運費為1050元,在(2)的條件下,若要使此次運費最少,應采取哪種方案?并求出最少的運費為多少元.
【答案】(1)采購了100條長條椅,200條弧型椅;(2)有三種方案,見解析;(3)最省錢的租車方案是租用A型卡車15輛、B型卡車5輛,最低運費為23250元.
【解析】試題分析:(1)設景區采購長條椅x條,弧型椅y條,然后根據游客人數和花費錢數兩個等量關系列出方程組求解即可;
(2)設租用A型卡車m輛,則租用B種卡車(20﹣m)輛,根據兩種型號卡車裝運的休閑椅的數量不小于兩種休閑椅的數量列出不等式組,求解即可,再根據車輛數是正整數寫出設計方案;
(3)設租車總費用為W元,列出W的表達式,再根據一次函數的增減性求出最少費用.
試題解析:解:(1)設景區采購長條椅x條,弧型椅y條,由題意得:
![]() ,解得:
,解得:![]() .
.
答:采購了100條長條椅,200條弧型椅;
(2)設租用A型卡車m輛,則租用B種卡車(20﹣m)輛,由題意得:![]() ,解得:15≤m≤17.5,由題意可知,m為正整數,所以,m只能取15、16、17,故有三種租車方案可一次性將這批休閑椅運回來,可這樣安排:
,解得:15≤m≤17.5,由題意可知,m為正整數,所以,m只能取15、16、17,故有三種租車方案可一次性將這批休閑椅運回來,可這樣安排:
方案一:A型卡車15輛,B型卡車5輛,方案二:A型卡車16輛,B型卡車4輛,方案三:A型卡車17輛,B型卡車3輛;
(3)設租車總費用為W元,則W=1200m+1050(20﹣m)=150m+21000.∵150>0,∴W隨m的增大而增大.又∵15≤m≤17.5,∴當m=15時,W有最小值,W最小=150×15+21000=23250,∴最省錢的租車方案是租用A型卡車15輛、B型卡車5輛,最低運費為23250元.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,動點P從點A出發沿AD方向向點D以1cm/s的速度運動,動點Q從點C開始沿著CB方向向點B以3cm/s的速度運動.點P、Q分別從點A和點C同時出發,當其中一點到達端點時,另一點隨之停止運動.
(1)經過多長時間,四邊形PQCD是平行四邊形?
(2)經過多長時間,四邊形PQBA是矩形?
(3)經過多長時間,當PQ不平行于CD時,有PQ=CD.

查看答案和解析>>
科目:初中數學 來源: 題型:
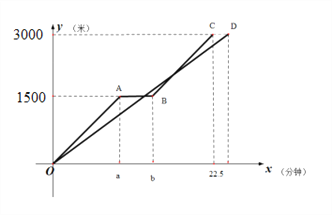
【題目】小軍和爸爸同時從家騎自行車去圖書館,爸爸先以150米/分的速度騎行一段時間,休息了5分鐘,再以m米/分的速度到達圖書館,小軍始終以同一速度騎行,兩人行駛的路程y(米)與時間x(分)的關系如圖所示,請結合圖像,解答下列問題:
(1)a= b= ,m=
(2)若小軍的速度是120米/分,求小軍在途中與爸爸第二次相遇時,距圖書館的距離;
(3)在(2)的條件下,爸爸自第二次出發至到達圖書館前,何時與小軍相距100米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,要在長方形和環形地塊中鋪設草坪,長方形的長、寬分別為a m、b m,環形的外圓、內圓的半徑分別為R m、r m.
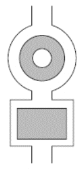
(1)求共需草皮的面積.
(2)若草皮每平方米需30元,當![]() 時,求草皮的費用.(保留π)
時,求草皮的費用.(保留π)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,任意一個正整數n都可以進行這樣的分解:![]() (
(![]() 、
、![]() 是正整數,且
是正整數,且![]() ).在n的所有這種分解中,如果
).在n的所有這種分解中,如果![]() 、
、![]() 兩因數之差的絕對值最小,我們就稱
兩因數之差的絕對值最小,我們就稱![]() 是n的最佳分解,并規定:
是n的最佳分解,并規定:![]() .例如12可以分解成
.例如12可以分解成![]() ,
,![]() 或
或![]() ,因為
,因為![]() ,所以
,所以![]() 是12的最佳分解,所以
是12的最佳分解,所以![]() .如果一個兩位正整數
.如果一個兩位正整數![]() ,
,![]() (
(![]() ,
,![]() 、
、![]() 為正整數),交換其個位上的數字與十位上的數字得到的新數減去原來的兩位正整數所得的差為18,那么我們稱這個數
為正整數),交換其個位上的數字與十位上的數字得到的新數減去原來的兩位正整數所得的差為18,那么我們稱這個數![]() 為“吉祥數”,則所有“吉祥數”中
為“吉祥數”,則所有“吉祥數”中![]() 的最大值為_____________.
的最大值為_____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=4,BC=6,E是BC邊的中點,點P在線段AD上,過P作PF⊥AE于F,設PA=x.
(1)求證:△PFA∽△ABE;
(2)當點P在線段AD上運動時,設PA=x,是否存在實數x,使得以點P,F,E為頂點的三角形也與△ABE相似?若存在,請求出x的值;若不存在,請說明理由;
(3)探究:當以D為圓心,DP為半徑的⊙D與線段AE只有一個公共點時,請直接寫出x滿足的條件: .

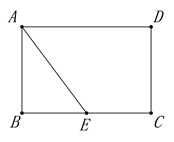
備用圖
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法:①兩個數互為倒數,則它們乘積為1;②若a、b互為相反數,則![]() =﹣1;③兩個四次單項式的和一定是四次多項式;④兩個有理數比較,絕對值大的反而小;⑤若a為任意有理數,則a﹣|a|≤0;⑥﹣5πR2的系數是﹣5.其中正確的有( )
=﹣1;③兩個四次單項式的和一定是四次多項式;④兩個有理數比較,絕對值大的反而小;⑤若a為任意有理數,則a﹣|a|≤0;⑥﹣5πR2的系數是﹣5.其中正確的有( )
A.2個B.3個C.4個D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某文教店購進一批鋼筆,按進價提高40%后標價,為了增加銷量,文教店決定按標價打八折出售,這時每支鋼筆的售價為28元.
(1)求每支鋼筆的進價為多少元;
(2)該文教店賣出這批鋼筆的一半后,決定將剩下的鋼筆以每3支80元的價格出售,很快銷售完畢,銷售這批鋼筆文教店共獲利2800元,求該文教店共購進這批鋼筆多少支?
查看答案和解析>>
科目:初中數學 來源: 題型:
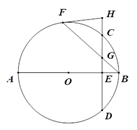
【題目】如圖,AB、BF分別是⊙O的直徑和弦,弦CD與AB、BF分別相交于點E、G,過點F的切線HF與DC的延長線相交于點H,且HF=HG.
(1)求證:AB⊥CD;
(2)若sin∠HGF=![]() ,BF=3,求⊙O的半徑長.
,BF=3,求⊙O的半徑長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com