
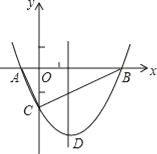
【題目】如圖,拋物線y=![]() x2+bx﹣2與x軸交于A、B兩點,與y軸交于C點,且A(一1,0).
x2+bx﹣2與x軸交于A、B兩點,與y軸交于C點,且A(一1,0).
(1)求拋物線的解析式及頂點D的坐標;
(2)判斷△ABC的形狀,證明你的結論;
(3)點M是拋物線對稱軸上的一個動點,當△ACM周長最小時,求點M的坐標及△ACM的最小周長.
【答案】(1)y=![]() x2-
x2-![]() x-2;(
x-2;(![]() , -
, -![]() );(2)△ABC是直角三角形;(3)
);(2)△ABC是直角三角形;(3)![]() ,△ACM最小周長是
,△ACM最小周長是![]() .
.
【解析】試題分析:(1)直接將(﹣1,0),代入解析式進而得出答案,再利用配方法求出函數頂點坐標;
(2)分別得出AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,進而利用勾股定理的逆定理得出即可;
(3)利用軸對稱最短路線求法得出M點位置,再求△ACM周長最小值.
解:(1)∵點A(﹣1,0)在拋物線y=![]() x2+bx﹣2上,
x2+bx﹣2上,
∴![]() ×(﹣1 )2+b×(﹣1)﹣2=0,
×(﹣1 )2+b×(﹣1)﹣2=0,
解得:b=﹣![]() ,
,
∴拋物線的解析式為y=![]() x2﹣
x2﹣![]() x﹣2.
x﹣2.
y=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() ,
,
∴頂點D的坐標為:(![]() ,﹣
,﹣![]() );
);
(2)當x=0時y=﹣2,∴C(0,﹣2),OC=2.
當y=0時,![]() x2﹣
x2﹣![]() x﹣2=0,
x﹣2=0,
解得:x1=﹣1,x2=4,
∴B (4,0),
∴OA=1,OB=4,AB=5.
∵AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,
∴AC2+BC2=AB2.
∴△ABC是直角三角形.
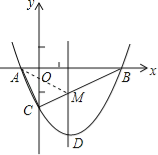
(3)如圖所示:連接AM,
點A關于對稱軸的對稱點B,BC交對稱軸于點M,根據軸對稱性及兩點之間線段最短可知,
MC+MA的值最小,即△ACM周長最小,
設直線BC解析式為:y=kx+d,則![]() ,
,
解得: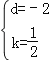 ,
,
故直線BC的解析式為:y=![]() x﹣2,
x﹣2,
當x=![]() 時,y=﹣
時,y=﹣![]() ,
,
∴M(![]() ,﹣
,﹣![]() ),
),
△ACM最小周長是:AC+AM+MC=AC+BC=![]() +2
+2![]() =3
=3![]() .
.


 期末集結號系列答案
期末集結號系列答案科目:初中數學 來源: 題型:
【題目】【問題提出】
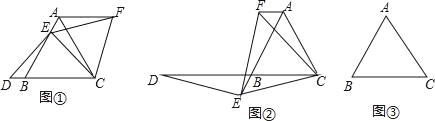
如圖①,已知△ABC是等腰三角形,點E在線段AB上,點D在直線BC上,且ED=EC,將△BCE繞點C順時針旋轉60°至△ACF連接EF
試證明:AB=DB+AF
【類比探究】
(1)如圖②,如果點E在線段AB的延長線上,其他條件不變,線段AB,DB,AF之間又有怎樣的數量關系?請說明理由
(2)如果點E在線段BA的延長線上,其他條件不變,請在圖③的基礎上將圖形補充完整,并寫出AB,DB,AF之間的數量關系,不必說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)用“*”表示一種新運算:對于任意正實數a,b,都有![]() .例如,
.例如,![]() ,那么15*27=__;(2)定義一種運算*,其規則為:當a≥b時,a*b=b3;當a<b時,a*b=b2.根據這個規則,方程3*x=27的解是__.
,那么15*27=__;(2)定義一種運算*,其規則為:當a≥b時,a*b=b3;當a<b時,a*b=b2.根據這個規則,方程3*x=27的解是__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為提供節約用水,某市按如下規定每月收取水費,若一戶居民每月用水不超過20立方米,則每立方米按3元收費;若超過20立方米,前20立方米收費標準不變,超過部分每立方米按5元收費,若某戶居民某月用水![]() 立方米.
立方米.
(1)試用含![]() (
(![]() >20)的代數式表示這戶居民該月應繳的水費.
>20)的代數式表示這戶居民該月應繳的水費.
(2)已知該市小李家1月份用水13立方米,2月份用水22立方米,3月份用水17立方米,求他家這三個月應繳納水費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小麗剪了一些直角三角形紙片,她取出其中的幾張進行了如下的操作:
操作一:如圖,將Rt△ABC沿某條直線折疊,使斜邊的兩個端點A與B重合,折痕為DE.
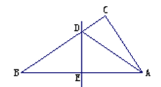
(1)如果AC=6cm,BC=8cm,試求△ACD的周長.
(2)如果∠CAD:∠BAD=4:7,求∠B的度數.
操作二:如圖,小麗拿出另一張Rt△ABC紙片,將直角邊AC沿直線AD折疊,使它落在斜邊AB上,且與AE重合,已知兩直角邊AC=6cm,BC=8cm,你能求出CD的長嗎?
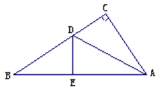
操作三:如圖,小麗又拿出另一張Rt△ABC紙片,將紙片折疊,折痕CD⊥AB。你能證明:BC2+AD2=AC2+BD2嗎?
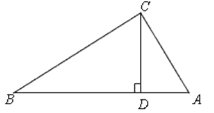
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD中,對角線AC=6,BD=8,M、N分別是BC、CD上的中點,P是線段BD上的一個動點,則PM+PN的最小值是( )
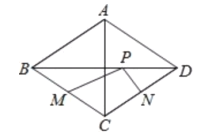
A.![]() B.3
B.3
C.![]() D.5
D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
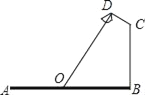
【題目】如圖,要在寬為22米的九州大道兩邊安裝路燈,路燈的燈臂CD長2米,且與燈柱BC成120°角,路燈采用圓錐形燈罩,燈罩的軸線DO與燈臂CD垂直,當燈罩的軸線DO通過公路路面的中心線時照明效果最佳,此時,路燈的燈柱BC高度應該設計為( )
A. (11﹣2![]() )米 B. (11
)米 B. (11![]() ﹣2
﹣2![]() )米 C. (11﹣2
)米 C. (11﹣2![]() )米 D. (11
)米 D. (11![]() ﹣4)米
﹣4)米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把幾個不同的數用大括號圍起來,中間用逗號斷開,如:{3,4},{-3,6,8,18},我們稱之為集合,其中大括號內的數稱其為集合的元素,如果一個集合滿足:只要其中有一個元素a,使得-2a+4也是這個集合的元素,這樣的集合我們稱為條件集合,例如:集合{3,2},因為-2×3+4=-2,-2恰好是這個集合的元素,所以{3,-2}是條件集合:例如:集合{-2,9,8},因為-2×(-2)+4=8,8恰好是這個集合的元素,所以{-2,9,8}是條件集合.
(1)集合{-4,12}______條件集合;集合{![]() ,-
,-![]() ,
,![]() }______條件集合 (填“是”或“不是”)
}______條件集合 (填“是”或“不是”)
(2)若集合{8,10,n}是條件集合,求n的所有可能值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】重慶格力廠為了檢驗甲、乙兩車間生產的同一款新產品的合格情況(尺寸r的范圍為176≤r≤185的產品為合格),隨機各抽取了20個樣品進行檢測,過程如下:
收集數據(單位:mm)
甲車間:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180
乙車間:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183
整理數據
級別 頻數 | 165.5~ 170.5 | 170.5~ 175.5 | 175.5~ 180.5 | 180.5~ 185.5 | 185.5 ~190.5 | 190.5~ 195.5 |
甲車間 | 2 | 4 | a | b | 2 | 1 |
乙車間 | 1 | 2 | 9 | 6 | 2 | 0 |
分析數據:
車間 | 平均數 | 眾數 | 中位數 | 方差 |
甲車間 | 180 | 185 | 180 | 43.1 |
乙車間 | 180 | 180 | c | 22.6 |
應用數據
(2)請寫出表中a= ,b= ,c= mm.
(2)估計甲車間生產的1000個該款新產品中合格產品有多少個?
(3)結合上述數據信息,請判斷哪個車間生產的新產品更好,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com