【題目】在平面直角坐標系
中，我們把橫 、縱坐標都是整數的點叫做整點．已知點
A（0，4），點B是
軸正半軸上的整點，記△AOB內部（不包括邊界）的整點個數為m．當m=3時，點B的橫坐標的所有可能值是 ▲ ；當點B的橫坐標為4n（n為正整數）時，m= （用含n的代數式表示．）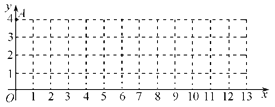
【答案】3或4；6n－3
【解析】
分類歸納（圖形的變化類），點的坐標，矩形的性質。
根據題意畫出圖形，再找出點B的橫坐標與△AOB內部（不包括邊界）的整點m之間的關系即可求出答案：
如圖：當點B在（3，0）點或（4，0）點時，△AOB內部（不包括邊界）的整點為（1，1），
（1，2），（2，1），共三個點，∴當m=3時，點B的橫坐標的所有可能值是3或4。
當點B的橫坐標為4n（n為正整數）時，
∵以OB為長OA為寬的矩形內（不包括邊界）的整點個數為（4n－1）×3="12" n－3，對角線AB上的整點個數總為3，
∴△AOB內部（不包括邊界）的整點個數m=（12 n－3－3）÷2=6n－3。
科目：初中數學 來源： 題型：
【題目】如圖，⊙O的直徑AB=4，C是⊙O上一點，連接OC．過點C作CD⊥AB，垂足為D，過點B作BM∥OC，在射線BM上取點E，使BE=BD，連接CE．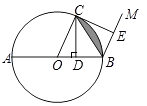 
（1）當∠COB=60°時，直接寫出陰影部分的面積；
（2）求證：CE是⊙O的切線．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在等腰Rt△ABC中，角ACB＝90°，P是線段BC上一動點（與點B，C不重合）連接AP，延長BC至點Q，使 CQ＝CP，過點Q作QH⊥AP于點H，交AB于點M．
(1)∠APC＝α，求∠AMQ的大小（用含α的式子表示）；
(2)在（1）的條件下，過點M作ME⊥QB于點E，試證明 PC 與 ME 之間的數量關系，并證明．
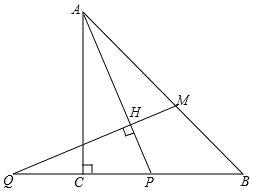
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠BAC=90°，∠B=60°，△AB′C′可以由△ABC繞點A順時針旋轉90°得到（點B′與點B是對應點，點C′與點C是對應點），連接CC′，則∠CC′B′的度數是 ．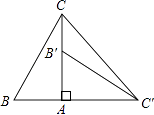 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】先化簡，再求值．
(1)(2x2y－4xy2)－(－
xy2＋x2y)，其中x＝－1，y＝2；
(2)2x2－[3(－
x2＋
xy)－2y2]－2(x2－xy＋2y2)，其中x，y滿足|x－|＋(y＋1)2＝0.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC中，∠C=90°，D是AC的中點，E是AB的中點，作EF⊥BC于F，延長BC至G，使CG=BF，連接CE、DE、DG．
（1）如圖1，求證：四邊形CEDG是平行四邊形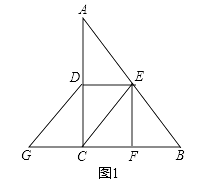 
；
（2）如圖2，連接EG交AC于點H，若EG⊥AB，請直接寫出圖2中所有長度等于 
GH的線段．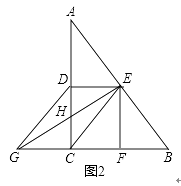 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為解決中小學大班額問題，東營市各縣區今年將改擴建部分中小學，某縣計劃對A、B兩類學校進行改擴建，根據預算，改擴建2所A類學校和3所B類學校共需資金7800萬元，改擴建3所A類學校和1所B類學校共需資金5400萬元．
（1）改擴建1所A類學校和1所B類學校所需資金分別是多少萬元？
（2）該縣計劃改擴建A、B兩類學校共10所，改擴建資金由國家財政和地方財政共同承擔．若國家財政撥付資金不超過11800萬元；地方財政投入資金不少于4000萬元，其中地方財政投入到A、B兩類學校的改擴建資金分別為每所300萬元和500萬元．請問共有哪幾種改擴建方案？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，在平行四邊形ABDC中，∠ABC的平分線交AD于點E，過點A作BE的垂線交BE于點F，交BC于點G，連接EG，CF．
（1）求證：四邊形AEGE是菱形；
（2）若∠ABC=60°，AB=4，AD=5，求CF的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
