【題目】如圖，在平面直角坐標系中，Rt△ABC的三個頂點分別是A（﹣3，2），B（0，4），C（0，2）．
（1）將△ABC以點C為旋轉中心旋轉180°，畫出旋轉后對應的△A1B1C；
（2）平移△ABC，若點A的對應點A2的坐標為（0，﹣4），畫出平移后對應的△A2B2C2 ；
（3）若將△A1B1C繞某一點旋轉可以得到△A2B2C2,請直接寫出旋轉中心的坐標 .
【答案】（1）圖略
（2）旋轉中心為（1．5，－1）
（3）P（－2，0）
【解析】（1）延長AC到A1，使得AC=A1C，延長BC到B1，使得BC=B1C，利用點A的對應點A2的坐標為（0，-4），得出圖象平移單位，即可得出△A2B2C2；
（2）根據△△A1B1C繞某一點旋轉可以得到△A2B2C2進而得出，旋轉中心即可；
（3）根據B點關于x軸對稱點為A2，連接AA2，交x軸于點P，再利用相似三角形的性質求出P點坐標即可．
解：（1）△A1B1C如圖所示，
△A2B2C2如圖所示；
（2）如圖，旋轉中心坐標為（1.5，3）；
（3）如圖所示，點P的坐標為（﹣2，0）．
“點睛”此題主要考查了圖形的平移與旋轉和相似三角形的性質等知識，利用軸對稱求最小值問題是考試重點，同學們應重點掌握．
科目：初中數學 來源： 題型：
【題目】小明和小莉在跑道上進行100 m短跑比賽，兩人從出發點同時起跑，小明到達終點時，小莉離終點還差6 m，已知小明和小莉的平均速度分別為x m/s、y m/s．
（1）如果兩人重新開始比賽，小明從起點向后退6 m，兩人同時起跑能否同時到達終點？若能，請求出兩人到達終點的時間；若不能，請說明誰先到達終點．
（2）如果兩人想同時到達終點，應如何安排兩人起跑位置？請設計兩種方案．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知AO為Rt△ABC的角平分線，∠ACB=90°，
，以O為圓心，OC 為半徑的圓分別交AO，BC于點D，E，連接ED并延長交AC于點F．
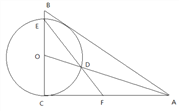
（1）求證：AB是⊙O的切線；
（2）求
的值。
（3）若⊙O的半徑為4，求
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某公司到果品基地購買某種優質水果慰問醫務工作者，果品基地對購買量在3000kg以上（含3000kg）的顧客采用兩種銷售方案.甲方案：每千克9元，由基地送貨上門；乙方案：每千克8元，由顧客自己租車運回.已知該公司租車從基地到公司的運輸費用為5000元.
（1）分別寫出該公司兩種購買方案付款金額y（元）與所購買的水果量x（kg）之間的函數關系式.
（2）當購買量在哪一范圍時，選擇哪種購買方案付款最少？并說明理由
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知x1，x2是一元二次方程（a﹣6）x2+2ax+a=0的兩個實數根．
（1）是否存在實數a，使﹣x1+x1x2=4+x2成立？若存在，求出a的值；若不存在，請你說明理由；
（2）求使（x1+1）（x2+1）為正整數的實數a的整數值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在正方形ABCD中，邊長為2的等邊三角形AEF的頂點E、F分別在BC和CD上，下列結論：①BE=DF；②∠AEB=75°；③CE=2；④S正方形ABCD=2+
，其中正確答案是（ ）
A.①②B.②③C.①②④D.①②③
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商店經銷一種雙肩包，已知這種雙肩包的成本價為每個30元．市場調查發現，這種雙肩包每天的銷售量y（單位:個）與銷售單價x（單位:元）有如下關系：y=－x+60（30≤x≤60）．
設這種雙肩包每天的銷售利潤為w元．
（1）求w與x之間的函數解析式；
（2）這種雙肩包銷售單價定為多少元時，每天的銷售利潤最大？最大利潤是多少元？
（3）如果物價部門規定這種雙肩包的銷售單價不高于48元，該商店銷售這種雙肩包每天要獲得200元的銷售利潤，銷售單價應定為多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】當﹣2＜x＜2時，下列函數中，函數值y隨自變量x增大而增大的有（ ）個．
①y=2x；②y=2﹣x；③y=﹣
；④y=x2+6x+8．
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com