
【題目】如圖,直線![]() 分別與
分別與![]() 軸,
軸,![]() 軸交于點
軸交于點![]() ,
,![]() ,過點
,過點![]() 的直線
的直線![]() 交
交![]() 軸于點
軸于點![]() .
.![]() 為
為![]() 的中點,
的中點,![]() 為射線
為射線![]() 上一動點,連結
上一動點,連結![]() ,
,![]() ,過
,過![]() 作
作![]() 于點
于點![]() .
.
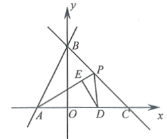
(1)直接寫出點![]() ,
,![]() 的坐標:
的坐標:![]() (______,______),
(______,______),![]() (______,______);
(______,______);
(2)當![]() 為
為![]() 中點時,求
中點時,求![]() 的長;
的長;
(3)當![]() 是以
是以![]() 為腰的等腰三角形時,求點
為腰的等腰三角形時,求點![]() 坐標;
坐標;
(4)當點![]() 在線段
在線段![]() (不與
(不與![]() ,
,![]() 重合)上運動時,作
重合)上運動時,作![]() 關于
關于![]() 的對稱點
的對稱點![]() ,若
,若![]() 落在
落在![]() 軸上,則
軸上,則![]() 的長為_______.
的長為_______.
【答案】(1)-2,0;2,0;(2)![]() ;(3)當
;(3)當![]() 或
或![]() 時,
時,![]() 是以
是以![]() 為腰的等腰三角形;(4)
為腰的等腰三角形;(4)![]() .
.
【解析】
(1)先根據![]() 求出A,B的坐標,再把B點坐標代入
求出A,B的坐標,再把B點坐標代入![]() 求出b值,即可求解C點坐標,再根據
求出b值,即可求解C點坐標,再根據![]() 為
為![]() 的中點求出D點坐標;
的中點求出D點坐標;
(2)先求出P點坐標得到![]() ,再根據
,再根據![]() 即可求解;
即可求解;
(3)根據題意分①![]() ②
②![]() ,即可列方程求解;
,即可列方程求解;
(4)根據題意作圖,可得對稱點![]() 即為A點,故AD=PD=4,設
即為A點,故AD=PD=4,設![]() ,作PF⊥AC于F點,得DF=2-x,PF=-x+4,利用Rt△PFD列方程解出x,得到P點坐標,再根據坐標間的距離公式即可求解.
,作PF⊥AC于F點,得DF=2-x,PF=-x+4,利用Rt△PFD列方程解出x,得到P點坐標,再根據坐標間的距離公式即可求解.
(1)由直線AB的解析式為![]() ,
,
令y=0,得x=-2,
∴![]() ,
,
令x=0,得y=4,∴B(0,4)
把B(0,4)代入![]() ,求得b=4,
,求得b=4,
∴直線BC的解析式為![]()
令y=0,得x=4,∴![]()
∵![]() 為
為![]() 的中點
的中點
∴![]()
故答案為:-2,0;2,0;
(2)由(1)得B(0,4),![]()
當![]() 為
為![]() 的中點時,則
的中點時,則![]() ,
,
∵![]() 為
為![]() 的中點,
的中點,
∴![]() 軸,
軸,
![]() ,
,![]() ,
,
∴![]()
∵![]() ,
,
∴![]()
(3)∵點![]() 是射線
是射線![]() 上一動點,設
上一動點,設![]() ,當
,當![]() 是以
是以![]() 為腰的等腰三角形時,
為腰的等腰三角形時,
①若![]() ,
,![]() ,解得:
,解得:![]() ,
,![]() (舍去),此時
(舍去),此時![]() ;
;
②若![]() ,
,![]() ,解得:
,解得:![]() ,此時
,此時![]() .
.
綜上,當![]() 或
或![]() 時,
時,![]() 是以
是以![]() 為腰的等腰三角形.
為腰的等腰三角形.
(4)∵![]() 關于
關于![]() 的對稱點
的對稱點![]() ,若
,若![]() 落在
落在![]() 軸上
軸上
∴點![]() 為A點,
為A點,
∴AD=PD=4,
設![]() ,作PF⊥AC于F點,
,作PF⊥AC于F點,
∴DF=2-x,PF=-x+4,
在Rt△PFD中,DF2+PF2=DP2
即(2-x)2+(-x+4)2=42
解得x=3-![]() (3+
(3+![]() 舍去)
舍去)
∴P(3-![]() ,
,![]() +1),
+1),
∴![]() =
=![]() =
=![]()
故答案為:![]() .
.


 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=﹣![]() x2+bx+c的圖象經過A(2,0),B(0,﹣6)兩點,
x2+bx+c的圖象經過A(2,0),B(0,﹣6)兩點,
(1)求這個二次函數的解析式;
(2)設該二次函數的對稱軸與x軸交于點C,連接BA,BC,求△ABC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
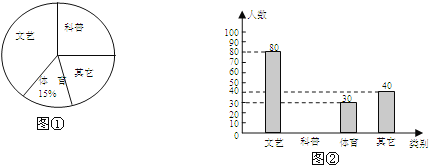
【題目】某校為了進一步豐富學生的課外閱讀,欲增購一些課外書,為此對該校一部分學生進行了一次“你最喜歡的書籍”問卷調查(每人只選一項).根據收集到的數據,繪制成如下統計圖(不完整):
請根據圖中提供的信息,完成下列問題:
(1)在這次問卷調查中,一共抽查了 名學生;并在圖中補全條形統計圖;
(2)如果全校共有學生1600名,請估計該校最喜歡“科普”書籍的學生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于等腰三角形,有以下說法:
(1)有一個角為![]() 的等腰三角形一定是銳角三角形
的等腰三角形一定是銳角三角形
(2)等腰三角形兩邊的中線一定相等
(3)兩個等腰三角形,若一腰以及該腰上的高對應相等,則這兩個等腰三角形全等
(4)等腰三角形兩底角的平分線的交點到三邊距離相等
其中,正確說法的個數為( )
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,如果點
厘米,如果點![]() 以
以![]() 厘米
厘米![]() 的速度運動.
的速度運動.

(1)如果點![]() 在線段
在線段![]() 上由點
上由點![]() 向點
向點![]() 運動.點
運動.點![]() 在線段
在線段![]() 上由
上由![]() 點向
點向![]() 點運動,它們同時出發,若點
點運動,它們同時出發,若點![]() 的運動速度與點
的運動速度與點![]() 的運動速度相等:
的運動速度相等:
①經過“![]() 秒后,
秒后,![]() 和
和![]() 是否全等?請說明理由.
是否全等?請說明理由.
②當兩點的運動時間為多少秒時,![]() 剛好是一個直角三角形?
剛好是一個直角三角形?
(2)若點![]() 的運動速度與點
的運動速度與點![]() 的運動速度不相等,點
的運動速度不相等,點![]() 從點
從點![]() 出發,點
出發,點![]() 以原來的運動速度從點
以原來的運動速度從點![]() 同時出發,都順時針沿
同時出發,都順時針沿![]() 三邊運動,經過
三邊運動,經過![]() 秒時點
秒時點![]() 與點
與點![]() 第一次相遇,則點
第一次相遇,則點![]() 的運動速度是__________厘米
的運動速度是__________厘米![]() 秒.(直接寫出答案)
秒.(直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,矩形ABCD的頂點D在反比例函數![]() (x<0)的圖象上,頂點B,C在x軸上,對角線AC的延長線交y軸于點E,連接BE,△BCE的面積是6,則k=_____.
(x<0)的圖象上,頂點B,C在x軸上,對角線AC的延長線交y軸于點E,連接BE,△BCE的面積是6,則k=_____.
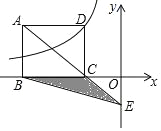
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的角平分線.
的角平分線.
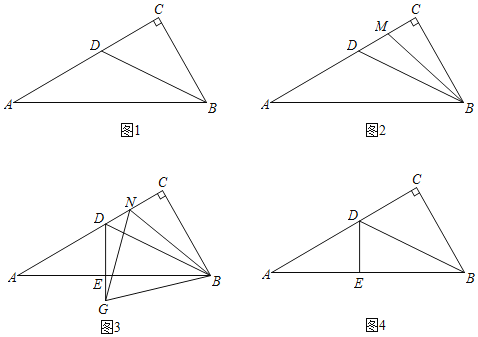
(1)如圖 1,求證:![]() ;
;
(2)如圖 2,作![]() 的角平分線交線段
的角平分線交線段![]() 于點
于點![]() ,若
,若![]() ,求
,求![]() 的面積;
的面積;
(3)如圖 3,過點![]() 作
作![]() 于點
于點![]() ,點
,點![]() 是線段
是線段![]() 上一點(不與
上一點(不與 ![]() 重合),以
重合),以![]() 為一邊,在
為一邊,在![]() 的下方作
的下方作![]() ,
,![]() 交
交![]() 延長線于點
延長線于點![]() ,試探究線段
,試探究線段![]() ,
,![]() 與
與![]() 之間的數量關系,并說明理由.
之間的數量關系,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com