
【題目】問題:如何快速計算1+2+3+…+n 的值呢?
(1)探究:令s=1+2+3+…+n①,則s=n+n-1+…+2+1②
①+②得2s=(n+1)(n+1)+…+(n+1)=n![]() (n+1)
(n+1)
因此![]() _________________.
_________________.
(2)應用:
①計算:![]() ________;
________;
②如圖1,一串連續的整數1,2,3,4,…,自上往下排列,最上面一行有一個數,以下各行均比上一行多一個數字,若共有15行數字,則最底下一行最左邊的數是_______;

③如圖2,一串連續的整數-25,-24,-23,…,按圖1方式排列,共有14行數字,求圖2中所有數字的和.
 天天練口算系列答案
天天練口算系列答案科目:初中數學 來源: 題型:
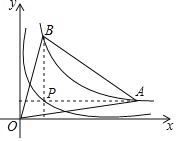
【題目】如圖,點P為函數y=![]() (x>0)圖象上一點過點P作x軸、y軸的平行線,分別與函數y
(x>0)圖象上一點過點P作x軸、y軸的平行線,分別與函數y![]() (x>0)的圖象交于點A,B,則△AOB的面積為_____.
(x>0)的圖象交于點A,B,則△AOB的面積為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
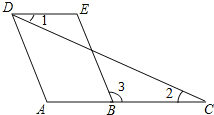
【題目】已知,如圖.AD∥BE,∠1=∠2,求證:∠A=∠E.請完成解答過程.
證明:∵AD∥BE(已知)
∴∠A=∠ ( )
又∵∠1=∠2(已知)
∴AC∥ ( )
∴∠3=∠ (兩直線平行,內錯角相等)
∴∠A=∠E(等量代換)
查看答案和解析>>
科目:初中數學 來源: 題型:
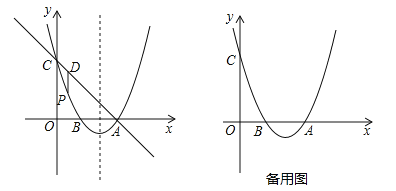
【題目】已知如圖,拋物線y=x2+bx+c過點A(3,0),B(1,0),交y軸于點C,點P是該拋物線上一動點,點P從C點沿拋物線向A點運動(點P不與點A重合),過點P作PD∥y軸交直線AC于點D.
(1)求拋物線的解析式;
(2)求點P在運動的過程中線段PD長度的最大值;
(3)△APD能否構成直角三角形?若能請直接寫出點P坐標,若不能請說明理由;
(4)在拋物線對稱軸上是否存在點M使|MA﹣MC|最大?若存在請求出點M的坐標,若不存在請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為創建足球特色學校,營造足球文化氛圍,某學校隨機抽取部分八年級學生足球運球的測試成績作為一個樣本,按A,B,C,D四個等級進行統計,制成了如下不完整的統計圖.(說明:A級:8分—10分,B級:7分—7.9分,C級:6分—6.9分,D級:1分—5.9分)根據所給信息,解答以下問題:
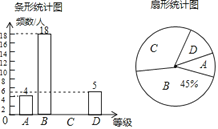
(1)樣本容量為 ,C對應的扇形的圓心角是____度,補全條形統計圖;
(2)所抽取學生的足球運球測試成績的中位數會落在____等級;
(3)該校八年級有300名學生,請估計足球運球測試成績達到![]() 級的學生有多少人?
級的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
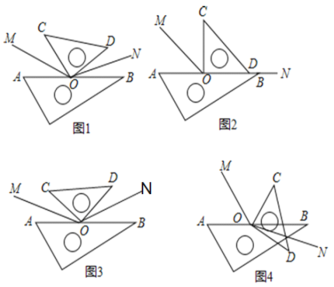
【題目】綜合與探究問題背景數學活動課上,老師將一副三角尺按圖(1)所示位置擺放,分別作出∠AOC,∠BOD的平分線OM、ON,然后提出如下問題:求出∠MON的度數.
特例探究“興趣小組”的同學決定從特例入手探究老師提出的問題,他們將三角尺分別按圖2、圖3所示的方式擺放,OM和ON仍然是∠AOC和∠BOD的角平分線.其中,按圖2方式擺放時,可以看成是ON、OD、OB在同一直線上.按圖3方式擺放時,∠AOC和∠BOD相等.
(1)請你幫助“興趣小組”進行計算:圖2中∠MON的度數為 °.圖3中∠MON的度數為 °.
發現感悟
解決完圖2,圖3所示問題后,“興趣小組”又對圖1所示問題進行了討論:
小明:由于圖1中∠AOC和∠BOD的和為90°,所以我們容易得到∠MOC和∠NOD的和,這樣就能求出∠MON的度數.
小華:設∠BOD為x°,我們就能用含x的式子分別表示出∠NOD和∠MOC度數,這樣也能求出∠MON的度數.
(2)請你根據他們的談話內容,求出圖1中∠MON的度數.
類比拓展
受到“興趣小組”的啟發,“智慧小組”將三角尺按圖4所示方式擺放,分別作出∠AOC、∠BOD的平分線OM、ON,他們認為也能求出∠MON的度數.
(3)你同意“智慧小組”的看法嗎?若同意,求出∠MON的度數;若不同意,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛出租車從![]() 地出發,在一條東西走向的街道上往返,每次行駛的路程(記向東為正)記錄如下表所示(
地出發,在一條東西走向的街道上往返,每次行駛的路程(記向東為正)記錄如下表所示(![]() ,單位:
,單位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 |
|
|
|
|
(1)寫出這輛出租車每次行駛的方向.
(2)求經過連續4次行駛后,這輛出租車所在的位置.
(3)這輛出租車一共行駛多少路程?
查看答案和解析>>
科目:初中數學 來源: 題型:
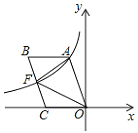
【題目】如圖,四邊形OABC是平行四邊形,邊OC在x軸的負半軸上,反比例函數![]() 的圖象經過點A與BC的中點F,連接AF,OF,若△AOF的面積為12,則k的值為_______.
的圖象經過點A與BC的中點F,連接AF,OF,若△AOF的面積為12,則k的值為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在四邊形ABCD中,AD//BC,對角線AC、BD交于點O,且AC=BD,下列四個命題中真命題是( )
A. 若AB=CD,則四邊形ABCD一定是等腰梯形;
B. 若∠DBC=∠ACB,則四邊形ABCD一定是等腰梯形;
C. 若![]() ,則四邊形ABCD一定是矩形;
,則四邊形ABCD一定是矩形;
D. 若AC⊥BD且AO=OD,則四邊形ABCD一定是正方形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com