
【題目】已知直線y1=﹣x+2和拋物線![]() 相交于點A,B.
相交于點A,B.
(1)當k=![]() 時,求兩函數圖象的交點坐標;
時,求兩函數圖象的交點坐標;
(2)二次函數y2的頂點為P,PA或PB與直線y1=﹣x+2垂直時,求k的值.
(3)當﹣4<x<2時,y1>y2,試直接寫出k的取值范圍.
【答案】(1)A(2,0),B(﹣![]() ,
,![]() );(2)1或-
);(2)1或-![]() ;(3)
;(3) ![]() <k<
<k<![]() 且k≠0.
且k≠0.
【解析】
(1)聯立方程組 即可求交點;
即可求交點;
(2)當PA與y1=-x+2垂直時,k=1;當PB與y1=-x+2垂直時,k=-![]() ;
;
(3)當x=-4時,y1>y2,6>24k;只有開口向上時成立,所以k>0;
(1)當k=![]() 時,
時,![]() ,
,
聯立方程組 ,
,
∴![]() 或
或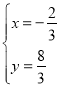 ,
,
∴A(2,0),B(﹣![]() ,
,![]() );
);
(2)![]() 的頂點P(1,﹣k),
的頂點P(1,﹣k),
當PA與y1=﹣x+2垂直時,k=1;
當PB與y1=﹣x+2垂直時,k=﹣![]() ;
;
(3)當x=2時,y1=y2=0,
當x=﹣4時,y1>y2,
當k>0時,
∴6>24k,
∴k<![]() ,
,
∴0<k<![]() ;
;
當k<0時,直線與拋物線有一個交點時:-x+2=kx2-2kx,
∵△=(1+2k)2=0,
∴k=![]() ,
,
∴![]() <k<0;
<k<0;
綜上所述;![]() <k<
<k<![]() 且k≠0;
且k≠0;


科目:初中數學 來源: 題型:
【題目】為了增強學生對新冠病毒預防知識的了解,我校初一年級開展了網上預防知識的宣傳教育活動.為了解這次宣傳教育活動的效果,學校從初一年級1500名學生中隨機抽取部分學生進行網上知識測試(測試滿分100分,得分均為整數),并根據抽取的學生測試成績,制作了如下統計圖表:
抽取學生知識測試成績的頻數表 | ||
成績 | 頻數(人) | 頻率 |
| 10 | 0.1 |
| 15 |
|
|
| 0.2 |
| 40 |
|
|
|
|
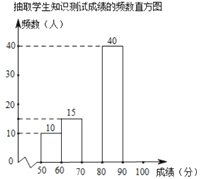
由圖表中給出的信息回答下列問題:
(1)![]() ,
,![]() ,并補全頻數直方圖;
,并補全頻數直方圖;
(2)如果80分以上(包括80分)為優秀,請估計初一年級1500名學生中成績優秀的人數;
(3)小強在這次測試中成績為85分,你認為85分一定是這100名學生知識測試成績的中位數嗎?請簡要說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】農夫將蘋果樹種在正方形的果園內,為了保護蘋果樹不受風吹,他在蘋果樹的周圍種上針葉樹.在下圖里,你可以看到農夫所種植蘋果樹的列數(n)和蘋果樹數量及針葉樹數量的規律:當n為某一個數值時,蘋果樹數量會等于針葉樹數量,則n為___________

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某專賣店有A、B兩種商品,已知在打折前,買60件A商品和30件B商品用了1080元,買50件A商品和10件B商品用了840元.A、B兩種商品打相同折以后,某人買500件A商品和450件B商品一共比不打折少花1960元,請問A、B兩種商品打折前各多少錢?打了多少折?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C是圓周上一點,連接AC、BC,以點C為端點作射線CD、CP分別交線段AB所在直線于點D、P,使∠1=∠2=∠A.

(1)求證:直線PC是⊙O的切線;
(2)若CD=4,BD=2,求線段BP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=ax+b的圖象與反比例函數![]() 的圖象交于C,D兩點,與x,y軸交于B,A兩點,且tan∠ABO=
的圖象交于C,D兩點,與x,y軸交于B,A兩點,且tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求一次函數的解析式和反比例函數的解析式;
(2)求△OCD的面積;
(3)根據圖象直接寫出一次函數的值大于反比例函數的值時,自變量x的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列結論:①abc>0;②2a+b=0;③若m為任意實數,則a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,則x1+x2=2.其中,正確結論的個數為( )
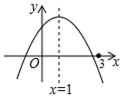
A.1B.2C.3D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com