
【題目】甲、乙兩家商場平時以同樣的價格出售相同的商品.“五一”節期間兩家商場都讓利酬賓.在甲商場按累計購物金額的![]() 收費;在乙商場累計購物金額超過
收費;在乙商場累計購物金額超過![]() 元后,超出
元后,超出![]() 元的部分按
元的部分按![]() 收費.設小紅在同一商場累計購物金額為
收費.設小紅在同一商場累計購物金額為![]() 元,其中
元,其中![]() .
.
(1)根據題意,填寫下表(單位:元):
累計購物金額 |
|
|
| ··· |
在甲商場實際花費 |
| ··· | ||
在乙商場實際花費 |
| ··· |
(2)設小紅在甲商場實際花費![]() 元,在乙商場實際花費
元,在乙商場實際花費![]() 元,分別求
元,分別求![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(3)“五一”節期間小紅如何選擇這兩家商場去購物更省錢?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)當小紅累計購物的金額超過600元時,在乙商場購物更省錢;當小紅累計購物的金額小于600元時,在甲商場購物更省錢.
;(3)當小紅累計購物的金額超過600元時,在乙商場購物更省錢;當小紅累計購物的金額小于600元時,在甲商場購物更省錢.
【解析】
(1)根據兩種購買方案即可求解;
(2)小紅在甲、乙兩商場的實際花費相同即可列方程求解;
(3)利用(1)所得代數式,分兩種情況列不等式求解.
解:(1)累計購物金額為500時,在甲商場實際花費:500×80%=400(元),
累計購物金額為900時,在甲商場實際花費:900×80%=720(元),
累計購物金額為500時,在乙商場實際花費: 200+(500-200)×70%=410(元),
累計購物金額為900時,在乙商場實際花費: 200+(900-200)×70%=690(元)
故答案為:![]()
(2)根據題意,![]()
![]()
(3)由0.8x<0.7x+60,解得x<600.
由0.8x>0.7x+60,解得x>600.
∴當小紅累計購物的金額超過600元時,在乙商場購物更省錢;
當小紅累計購物的金額小于600元時,在甲商場購物更省錢.


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案科目:初中數學 來源: 題型:
【題目】為調查廣西北部灣四市市民上班時最常用的交通工具的情況,隨機抽取了四市部分市民進行調查,要求被調查者從“A:自行車,B:電動車,C:公交車,D:家庭汽車,E:其他”五個選項中選擇最常用的一項,將所有調查結果整理后繪制成如下不完整的條形統計圖和扇形統計圖,請結合統計圖回答下列問題:

(1)在這次調查中,一共調查了 名市民,扇形統計圖中,C組對應的扇形圓心角是 °;
(2)請補全條形統計圖;
(3)若甲、乙兩人上班時從A、B、C、D四種交通工具中隨機選擇一種,則甲、乙兩人恰好選擇同一種交通工具上班的概率是多少?請用畫樹狀圖或列表法求解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】星期天8:00~8:30,燃氣公司給平安加氣站的儲氣罐注入天然氣,注完氣后,一位工作人員以每車20米![]() 的加氣量,依次給在加氣站排隊等候的若干輛車加氣儲氣罐中的儲氣量
的加氣量,依次給在加氣站排隊等候的若干輛車加氣儲氣罐中的儲氣量![]() (米
(米![]() )與時間
)與時間![]() (小時)的函數關系式如圖所示:
(小時)的函數關系式如圖所示:
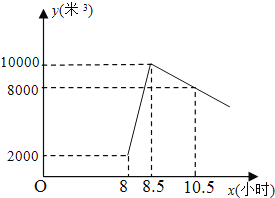
(1)8:00~8:30,燃氣公司向儲氣罐注入了______米![]() 的天然氣;
的天然氣;
(2)當![]() 時,求儲氣罐中的儲氣量(米
時,求儲氣罐中的儲氣量(米![]() )與時間
)與時間![]() (小時)的函數關系式;
(小時)的函數關系式;
(3)正在排隊等候的第20輛車加完后儲氣罐內還有天然氣______米![]() ,這20輛車在當天9:00之前能加完氣嗎?請說明理由.
,這20輛車在當天9:00之前能加完氣嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C地在A地的正東方向,因有大山阻隔,由A地到C地需要繞行B地,已知B地位于A地北偏東67°方向,距離A地520km,C地位于B地南偏東30°方向,若打通穿山隧道,建成兩地直達高鐵,求A地到C地之間高鐵線路的長(結果保留整數)(參考數據:sin67°≈0.92;cos67°≈0.38;![]() ≈1.73)
≈1.73)
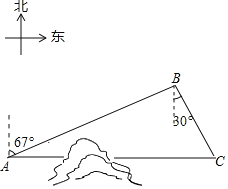
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】五一前夕,某時裝店老板到廠家選購![]() 兩種品牌的時裝,若購進
兩種品牌的時裝,若購進![]() 品牌的時裝
品牌的時裝![]() 套,
套,![]() 品牌的時裝
品牌的時裝![]() 套,需要
套,需要![]() 元;若購進
元;若購進![]() 品牌的時裝
品牌的時裝![]() 套,
套,![]() 品牌的時裝
品牌的時裝![]() 套,需要
套,需要![]() 元.
元.
(1)求![]() 兩種品牌的時裝每套進價分別為多少元?
兩種品牌的時裝每套進價分別為多少元?
(2)若![]() 套
套![]() 品牌的時裝售價
品牌的時裝售價![]() 元,
元,![]() 套
套![]() 品牌的時裝售價
品牌的時裝售價![]() 元,時裝店將購進的
元,時裝店將購進的![]() 兩種時裝共
兩種時裝共![]() 套全部售出,所獲利潤要不少于
套全部售出,所獲利潤要不少于![]() 元,問
元,問![]() 品牌時裝至少購進多少套?
品牌時裝至少購進多少套?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在矩形ABCD內,將兩張邊長分別為a和b(a>b)的正方形紙片按圖1,圖2兩種方式放置(圖1,圖2中兩張正方形紙片均有部分重疊),矩形中未被這兩張正方形紙片覆蓋的部分用陰影表示,設圖2中陰影部分的周長與圖1中陰影部分的周長的差為l,若要知道l的值,只要測量圖中哪條線段的長( )
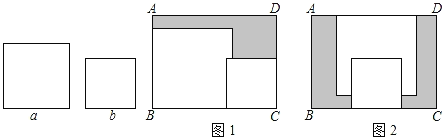
A.aB.bC.ADD.AB
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明星期天上午8:00從家出發到離家36千米的書城買書,他先從家出發騎公共自行車到公交車站,等了12分鐘的車,然后乘公交車于9:48分到達書城(假設在整個過程中小明騎車的速度不變,公交車勻速行駛,小明家、公交車站、書城依次在一條筆直的公路旁).如圖是小明從家出發離公交車站的路程y(千米)與他從家出發的時間x(時)之間的函數圖象,其中線段AB對應的函教表達式為y=kx+6.
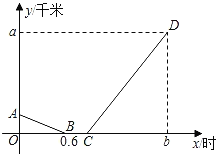
(1)求小明騎公共自行車的速度;
(2)求線段CD對應的函數表達式;
(3)求出發時間x在什么范圍時,小明離公交車站的路程不超過3千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,扇形OAB中,∠AOB=90°,將扇形OAB繞點B逆時針旋轉,得到扇形BDC,若點O剛好落在弧AB上的點D處,則![]() 的值為( )
的值為( )
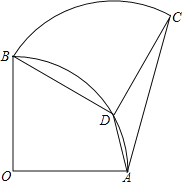
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,CD是△ABC的中線,如果![]() 上的所有點都在△ABC的內部或邊上,則稱
上的所有點都在△ABC的內部或邊上,則稱![]() 為△ABC的中線弧.
為△ABC的中線弧.
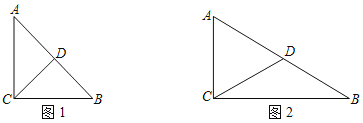
(1)在Rt△ABC中,∠ACB=90°,AC=1,D是AB的中點.
①如圖1,若∠A=45°,畫出△ABC的一條中線弧![]() ,直接寫出△ABC的中線弧
,直接寫出△ABC的中線弧![]() 所在圓的半徑r的最小值;
所在圓的半徑r的最小值;
②如圖2,若∠A=60°,求出△ABC的最長的中線弧![]() 的弧長l.
的弧長l.
(2)在平面直角坐標系中,已知點A(2,2),B(4,0),C(0,0),在△ABC中,D是AB的中點.求△ABC的中線弧![]() 所在圓的圓心P的縱坐標t的取值范圍.
所在圓的圓心P的縱坐標t的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com