
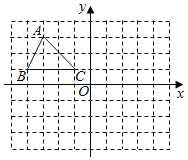
【題目】如圖,已知A(﹣3,3)、B(﹣4,1)、C(﹣1,1)是平面直角坐標系上的三點.
(1)請畫出△ABC繞點O逆時針旋轉90°后的△A1B1C1;
(2)請畫出△A1B1C1關于y軸對稱△A2B2C2;
(3)判斷以A、A1、A2為頂點的三角形的形狀.(無需說明理由)
科目:初中數學 來源: 題型:
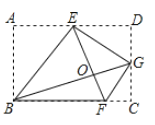
【題目】將矩形ABCD按如圖所示的方式折疊,BE,EG,FG為折痕,若頂點A,C,D都落在點O處,且點B,O,G在同一條直線上,同時點E,O,F在另一條直線上,則![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
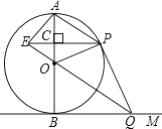
【題目】如圖,![]() 是
是![]() 的直徑,
的直徑,![]() 切
切![]() 于點
于點![]() ,點
,點![]() 是
是![]() 上的一個動點(點
上的一個動點(點![]() 不與
不與![]() ,
,![]() 兩點重合),連接
兩點重合),連接![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,交
,交![]() 的延長線于點
的延長線于點![]() ,連接
,連接![]() ,
,![]() ,
,![]() .
.
(1)求證:直線![]() 為
為![]() 的切線;
的切線;
(2)若直徑![]() 的長為4.
的長為4.
①當![]() ________時,四邊形
________時,四邊形![]() 為正方形;
為正方形;
②當![]() ________時,四邊形
________時,四邊形![]() 為菱形.
為菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)問題發(fā)現
如圖1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,連接AC,BD交于點M.填空:
①![]() 的值為 ;
的值為 ;
②∠AMB的度數為 .
(2)類比探究
如圖2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,連接AC交BD的延長線于點M.請判斷![]() 的值及∠AMB的度數,并說明理由;
的值及∠AMB的度數,并說明理由;
(3)拓展延伸
在(2)的條件下,將△OCD繞點O在平面內旋轉,AC,BD所在直線交于點M,若OD=1,OB=![]() ,請直接寫出當點C與點M重合時AC的長.
,請直接寫出當點C與點M重合時AC的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
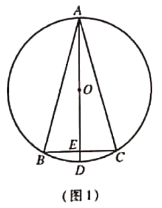
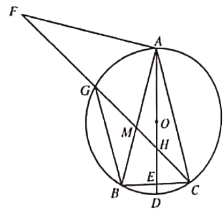
【題目】已知:![]() 是
是![]() 的內接三角形,且
的內接三角形,且![]() ,直徑
,直徑![]() 交
交![]() 于點
于點![]() .
.
![]() 如圖1 ,求證:
如圖1 ,求證:![]() ;
;
![]() 如圖2,將線段
如圖2,將線段![]() 繞點
繞點![]() 順時針旋轉得到線段
順時針旋轉得到線段![]() ,旋轉角為
,旋轉角為![]() 連接
連接![]() 分別交
分別交![]() ,
,![]() 于點
于點![]() ,連接
,連接![]() ,求證:
,求證: ![]() ;
;
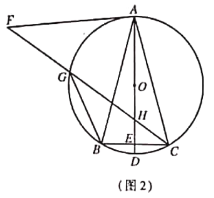
![]() 如圖3,在(2)的條件下,當
如圖3,在(2)的條件下,當![]() 時,
時,![]() 交
交![]() 于點
于點![]() 若
若![]() 求
求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】央視舉辦的《中國詩詞大會》受到廣大學生群體廣泛關注.某校的詩歌朗誦社團就《中國詩詞大會》節(jié)目的喜愛程度,在校內對部分學生進行了問卷調查,并對問卷調查的結果分為“非常喜歡”、“比較喜歡”、“感覺一般”、“不太喜歡”四個等級,分別記作A、B、C、D.根據調查結果繪制出如圖所示的扇形統(tǒng)計圖和條形統(tǒng)計圖,請結合圖中說給信息解答下列問題:
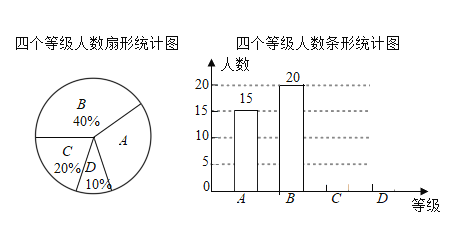
(1)本次被調查對象共有 人,扇形統(tǒng)計圖中被調查者“非常喜歡”等級所對應圓心角的度數為 ;
(2)將條形統(tǒng)計圖補充完整,并標明數據;
(3)若選“不太喜歡”的人中有兩名女生,其余是男生,從原“不太喜歡”的人中挑選兩名學生了解不太喜歡的原因,請用畫樹狀圖或列表法求所選取的這兩名學生恰好是一男一女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
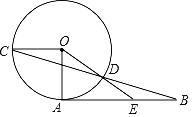
【題目】如圖,AB是⊙O的切線,OA,OC是⊙O的半徑,且OC∥AB,連接BC交⊙O于點D,點D恰為BC的中點,連接OD并延長,交AB于點E.
(1)求∠B的度數;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某書店以![]() 元的價格購進一批科普書進行銷售,物價局根據市場行情規(guī)定,銷售單價不低于
元的價格購進一批科普書進行銷售,物價局根據市場行情規(guī)定,銷售單價不低于![]() 元且不高于
元且不高于![]() 元.在銷售中發(fā)現,該科普書的每天銷售數量
元.在銷售中發(fā)現,該科普書的每天銷售數量![]() (本)與銷售單價
(本)與銷售單價![]() (元)之間存在某種函數關系,對應如下:
(元)之間存在某種函數關系,對應如下:
銷售單價 |
|
|
|
|
|
銷售數量 |
|
|
|
|
|
(1)用你所學過的函數知識,求出![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)請問該科普書每天利潤![]() (元)的最大值是多少?
(元)的最大值是多少?
(3)如果該科普書每天利潤必須不少于![]() 元,試求出每天銷售數量
元,試求出每天銷售數量![]() 最少為多少本?
最少為多少本?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】滴滴快車是一種便捷的出行工具,某地的計價規(guī)則如表:
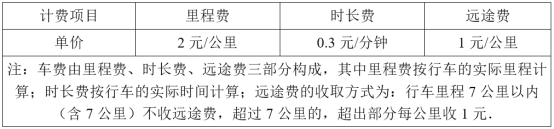
小李與小張分別從不同地點,各自同時乘坐滴滴快車,到同一地點相見,已知到達約定地點時他們的實際行車里程分別為7公里與9公里,兩人付給滴滴快車的乘車費相同.其中一人先到達約定地點,他等候另一人的時間等于他自己實際乘車時間,且恰好是另一人實際乘車時間的一半,則小李的乘車費為_____元.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com