
【題目】如圖,已知AB是⊙O的直徑,點D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.
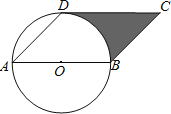
(1)判斷直線CD與⊙O的位置關系,并說明理由;
(2)若⊙O的半徑為1,求圖中陰影部分的周長.
【答案】(1)直線CD與⊙O相切,理由見解析;(2)2+![]() +
+![]()
【解析】
(1)直線與圓的位置關系無非是相切或不相切,可連接OD,證OD是否與CD垂直即可.
(2)陰影部分的周長可由CD+BC+扇形OBD的弧長求得;扇形的半徑和圓心角已求得,那么關鍵是求出平行四邊形CD的長,可通過證四邊形ABCD是平行四邊形,得出CD=AB,由此可求出CD的長,即可得解.
解:(1)直線CD與⊙O相切.理由如下:
如圖,連接OD,
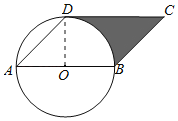
∵OA=OD,∠DAB=45°,
∴∠ODA=45°,
∴∠AOD=90°,
∵CD∥AB,
∴∠ODC=∠AOD=90°,即OD⊥CD,
又∵點D在⊙O上,
∴直線CD與⊙O相切;
(2)∵⊙O的半徑為1,AB是⊙O的直徑,
∴AB=2,
∵BC∥AD,CD∥AB,
∴四邊形ABCD是平行四邊形,
∴CD=AB=2,
由(1)知:△AOD是等腰直角三角形,
∵OA=OD=1,
∴BC=AD=![]() ,
,
∴圖中陰影部分的周長=CD+BC+![]() =2+
=2+![]() +
+![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,![]() 為
為![]() 的直徑,
的直徑,![]() 于點
于點![]() ,
,![]() 是
是![]() 上一點,且
上一點,且![]() ,延長
,延長![]() 至點
至點![]() ,連接
,連接![]() ,使
,使![]() ,延長
,延長![]() 與
與![]() 交于點
交于點![]() ,連結
,連結![]() ,
,![]() .
.
(1)連結![]() ,求證:
,求證:![]() ;
;
(2)求證:![]() 是
是![]() 的切線;
的切線;
(3)若![]() ,
,![]() ,求
,求![]() 的值.
的值.
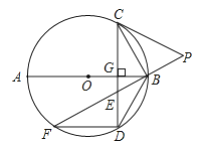
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司計劃購買2臺機器,該種機器使用三年后即被淘汰.機器有一易損零件,在購進機器時,可以額外購買這種零件作為備件,每個200元.在機器使用期間,如果備件不足再購買,則每個500元,三年后如果備件多余,每個以![]() 元(
元(![]() )回收.現需決策在購買機器時應同時購買幾個易損零件,為此搜集并整理了100臺這種機器在三年使用期內更換的易損零件數,得到如下頻數分布直方圖:
)回收.現需決策在購買機器時應同時購買幾個易損零件,為此搜集并整理了100臺這種機器在三年使用期內更換的易損零件數,得到如下頻數分布直方圖:
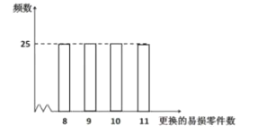
記![]() 表示2臺機器三年內共需更換的易損零件數,
表示2臺機器三年內共需更換的易損零件數,![]() 表示購買2臺機器的同時購買的易損零件數.
表示購買2臺機器的同時購買的易損零件數.
(1)以100臺機器為樣本,請利用畫樹狀圖或列表的方法估計![]() 不超過19的概率;
不超過19的概率;
(2)以這100臺機器在購買易損零件上所需費用的平均數為決策依據,在![]() 與
與![]() 之中選其一,當
之中選其一,當![]() 為何值時,選
為何值時,選![]() 比較劃算?
比較劃算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的盒子里裝有4個標有1,2,3,4的小球,它們形狀、大小完全相同.小明從盒子里隨機取出一個小球,記下球上的數字,作為點P的橫坐標x,放回然后再隨機取出一個小球,記下球上的數字,作為點P的縱坐標y.
(1)畫樹狀圖或列表,寫出點P所有可能的坐標;
(2)求出點P在以原點為圓心,5為半徑的圓上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小明設計的“過直線外一點作這條直線的平行線”的尺規作圖過程.
已知:如圖1,直線BC及直線BC外一點P.
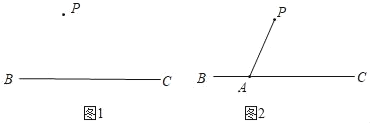
求作:直線PE,使得PE∥BC.
作法:如圖2.
①在直線BC上取一點A,連接PA;
②作∠PAC的平分線AD;
③以點P為圓心,PA長為半徑畫弧,交射線AD于點E;
④作直線PE.
所以直線PE就是所求作的直線.根據小明設計的尺規作圖過程.
(1)使用直尺和圓規,補全圖形(保留作圖痕跡);
(2)完成下面的證明.
證明:∵AD平分∠PAC,
∴∠PAD=∠CAD.
∵PA=PE,
∴∠PAD= ,
∴∠PEA= ,
∴PE∥BC.( )(填推理依據).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形OABC的一個頂點O是平面直角坐標系的原點,頂點A,C分別在y軸和x軸上,P為邊OC上的一個動點,且PQ⊥BP,PQ=BP,當點P從點C運動到點O時,可知點Q始終在某函數圖象上運動,則其函數圖象是( )
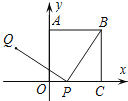
A.線段B.圓弧
C.雙曲線的一部分D.拋物線的一部分
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(感知)如圖①,正方形![]() 中,點
中,點![]() 在
在![]() 邊上,
邊上,![]() 平分
平分![]() .若我們分別延長
.若我們分別延長![]() 與
與![]() ,交于點
,交于點![]() ,則易證
,則易證![]() .(不需要證明)
.(不需要證明)
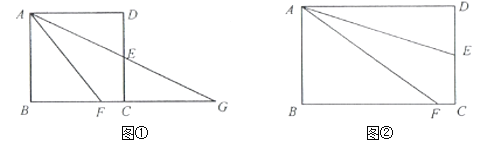
(探究)如圖②,在矩形![]() 中,點
中,點![]() 在
在![]() 邊的中點,點
邊的中點,點![]() 在
在![]() 邊上,
邊上,![]() 平分
平分![]() .求證:
.求證:![]() .
.
(應用)在(探究)的條件下,若![]() ,
,![]() ,直接寫出
,直接寫出![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】知,拋物線![]() (a
(a![]() 0)的頂點為A(s,t)(其中s
0)的頂點為A(s,t)(其中s![]() 0) .
0) .
(1)若拋物線經過(2,2)和(-3,37)兩點,且s=3.
①求拋物線的解析式;
②若n>3, 設點M(![]() ),N(
),N(![]() )在拋物線上,比較
)在拋物線上,比較![]() ,
,![]() 的大小關系,并說明理由;
的大小關系,并說明理由;
(2)若a=2,c=-2,直線![]() 與拋物線
與拋物線![]() 的交于點P和點Q,點P的橫坐標為h,點Q的橫坐標為h+3,求出b和h的函數關系式;
的交于點P和點Q,點P的橫坐標為h,點Q的橫坐標為h+3,求出b和h的函數關系式;
(3)若點A在拋物線![]() 上,且2≤s<3時,求a的取值范圍.
上,且2≤s<3時,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com