
【題目】夾在兩條平行線(xiàn)間的正方形ABCD、等邊三角形DEF如圖所示,頂點(diǎn)A、F分別在兩條平行線(xiàn)上.若A、D、F在一條直線(xiàn)上,則∠1與∠2的數(shù)量關(guān)系是( )

A. ∠1+∠2=60° B. ∠2﹣∠1=30° C. ∠1=2∠2. D. ∠1+2∠2=90°
【答案】B
【解析】
如圖,由AM//FN,可得∠1+∠BAD=∠DFE+∠2,再根據(jù)正方形的性質(zhì)、等邊三角形的性質(zhì)可得∠BAD=90°,∠DFE=60°,由此即可得∠1、∠2的關(guān)系.
如圖,∵AM//FN,
∴∠MAF=∠AFN,
即∠1+∠BAD=∠DFE+∠2,
∵四邊形ABCD是正方形,三角形DEF是等邊三角形,
∴∠BAD=90°,∠DFE=60°,
∴∠1+90°=60°+∠2,
∴∠2-∠1=30°,
故選B.


 期末1卷素質(zhì)教育評(píng)估卷系列答案
期末1卷素質(zhì)教育評(píng)估卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,∠C=90°,AD平分∠BAC,DE⊥AB于點(diǎn)E,有下列結(jié)論:①CD=ED ;②AC+ BE= AB ;③DA平分∠CDE ;④∠BDE =∠BAC;⑤![]() =AB:AC.其中結(jié)論正確的個(gè)數(shù)有()
=AB:AC.其中結(jié)論正確的個(gè)數(shù)有()
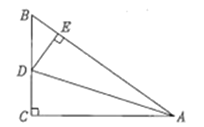
A.5個(gè)B.4個(gè)
C.3個(gè)D.2個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】今年4月18日﹣4月20日,第29屆重慶市青少年科技創(chuàng)新大賽在重慶南開(kāi)中學(xué)舉行,該校學(xué)生會(huì)在賽后對(duì)某年級(jí)各班的志愿者人數(shù)進(jìn)行了統(tǒng)計(jì),各班志愿者人數(shù)有6名、5名、4名、3名、2名、1名共計(jì)六種情況,并制成兩幅不完整的統(tǒng)計(jì)圖如下:
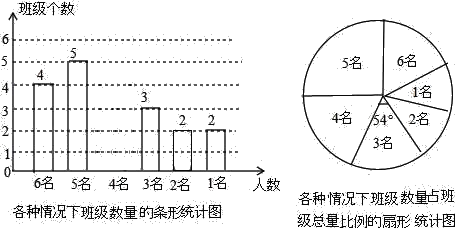
(1)該年級(jí)共有 個(gè)班級(jí),并將條形圖補(bǔ)充完整;
(2)求平均每班有多少名志愿者;
(3)為了了解志愿者在這次活動(dòng)中的感受,校學(xué)生會(huì)準(zhǔn)備從只有2名志愿者的班級(jí)中任選兩名志愿者參加座談會(huì),請(qǐng)用列表或畫(huà)樹(shù)狀圖的方法,求出所選志愿者來(lái)自同一個(gè)班級(jí)的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
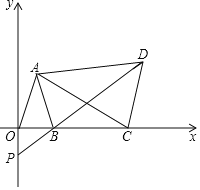
【題目】如圖,在xOy中,已知點(diǎn)A(a﹣1,a+b),B(a,0),且![]() =0,C為x軸上B點(diǎn)右側(cè)的動(dòng)點(diǎn),以AC為腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,DB交y軸于點(diǎn)P.
=0,C為x軸上B點(diǎn)右側(cè)的動(dòng)點(diǎn),以AC為腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,DB交y軸于點(diǎn)P.
(1)求A、B兩點(diǎn)坐標(biāo);
(2)求證:AO=AB;
(3)求證:∠OBP=∠OAB.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在ABCD中,AM,CN分別是∠BAD和∠BCD的平分線(xiàn),添加一個(gè)條件,仍無(wú)法判斷四邊形AMCN為菱形的是( )

A.AM=AN B.MN⊥AC
C.MN是∠AMC的平分線(xiàn) D.∠BAD=120°
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】一工地計(jì)劃租用甲、乙兩輛車(chē)清理淤泥,從運(yùn)輸量來(lái)估算,若租兩車(chē)合運(yùn),10天可以完成任務(wù),若甲車(chē)的效率是乙車(chē)效率的2倍.
![]() 甲、乙兩車(chē)單獨(dú)完成任務(wù)分別需要多少天?
甲、乙兩車(chē)單獨(dú)完成任務(wù)分別需要多少天?
![]() 已知兩車(chē)合運(yùn)共需租金65000元,甲車(chē)每天的租金比乙車(chē)每天的租金多1500元
已知兩車(chē)合運(yùn)共需租金65000元,甲車(chē)每天的租金比乙車(chē)每天的租金多1500元![]() 試問(wèn):租甲乙車(chē)兩車(chē)、單獨(dú)租甲車(chē)、單獨(dú)租乙車(chē)這三種方案中,哪一種租金最少?請(qǐng)說(shuō)明理由.
試問(wèn):租甲乙車(chē)兩車(chē)、單獨(dú)租甲車(chē)、單獨(dú)租乙車(chē)這三種方案中,哪一種租金最少?請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在![]() 和
和![]() 中,
中,![]() ,還需再添加兩個(gè)條件才能使
,還需再添加兩個(gè)條件才能使![]() ,則不能添加的一組條件是( )
,則不能添加的一組條件是( )

A. AC=DE,∠C=∠EB. BD=AB,AC=DE
C. AB=DB,∠A=∠DD. ∠C=∠E,∠A=∠D
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】探究:如圖,分別以△ABC的兩邊AB和AC為邊向外作正方形ABMN和正方形ACDE,CN、BE交于點(diǎn)P. 求證:∠ANC = ∠ABE.
應(yīng)用:Q是線(xiàn)段BC的中點(diǎn),連結(jié)PQ. 若BC = 6,則PQ = ___________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,它的周長(zhǎng)為
,它的周長(zhǎng)為![]() .若
.若![]() 與
與![]() ,
,![]() ,
,![]() 三邊分別切于
三邊分別切于![]() ,
,![]() ,
,![]() 點(diǎn),則
點(diǎn),則![]() 的長(zhǎng)為( )
的長(zhǎng)為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com