
【題目】如圖,某風景區內有一瀑布,AB表示瀑布的垂直高度,在與瀑布底端同一水平位置的點D處測得瀑布頂端A的仰角β為45°,沿坡度i=1:3的斜坡向上走100米,到達觀景臺C,在C處測得瀑布頂端A的仰角α為37°,若點B、D、E在同一水平線上.(參考數據:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈3.16)
≈3.16)
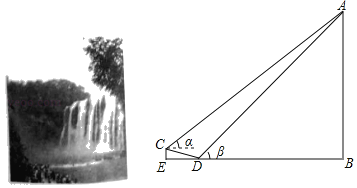
(1)觀景臺的高度CE為 米(結果保留準確值);
(2)求瀑布的落差AB(結果保留整數).
【答案】(1)10![]() ;(2)瀑布的落差約為411米.
;(2)瀑布的落差約為411米.
【解析】
(1)通過解直角△CDE得到:CE=CDsin37°.
(2)作CF⊥AB于F,構造矩形CEBF.由矩形的性質和解直角△ADB得到DE的長度,最后通過解直角△ACF求得答案.
(1)∵tan∠CDE=![]()
∴CD=3CE.
又CD=100米,
∴100=![]()
∴CE=10![]() .
.
故答案是:10![]() .
.
(2)作CF⊥AB于F,則四邊形CEBF是矩形.
∴CE=BF=10![]() ,CF=BE.
,CF=BE.
在直角△ADB中,∠DB=45°.設AB=BD=x米.
∵![]() =
=![]() ,
,
∴DE=30![]() .
.
在直角△ACF中,∠ACF=37°,tan∠ACF![]()
解得x≈411.
答:瀑布的落差約為411米.


科目:初中數學 來源: 題型:
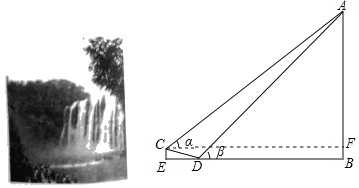
【題目】如圖,![]() 是
是![]() 的直徑,點
的直徑,點![]() 是弧
是弧![]() 上一點,且
上一點,且![]() ,
,![]() 與
與![]() 交與點
交與點![]() .
.
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)若![]() 平分
平分![]() ,求證:
,求證:![]() ;
;
(3)在(2)的條件下,延長![]() ,
,![]() 交于點
交于點![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的長和
的長和![]() 的半徑.
的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】端午節是我國的傳統節日,人們素有吃粽子的習俗,某商場在端午節來臨之際用3000元購進![]() 、
、![]() 兩種粽子1100個,購買
兩種粽子1100個,購買![]() 種粽子與購買
種粽子與購買![]() 種粽子的費用相同,已知
種粽子的費用相同,已知![]() 粽子的單價是
粽子的單價是![]() 種粽子單價的1.2倍.
種粽子單價的1.2倍.
(1)求![]() 、
、![]() 兩種粽子的單價各是多少?
兩種粽子的單價各是多少?
(2)若計劃用不超過7000元的資金再次購買![]() 、
、![]() 兩種粽子共2600個,已知
兩種粽子共2600個,已知![]() 、
、![]() 兩種粽子的進價不變,求
兩種粽子的進價不變,求![]() 中粽子最多能購進多少個?
中粽子最多能購進多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是拋物線y=ax2+bx+c(a≠0)的部分圖象,其頂點坐標為(1,n),且與x軸的一個交點在點(3,0)和(4,0)之間.則下列結論:①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有兩個不相等的實數根.其中正確結論的是______________(只填序號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在小正方形組成網格圖中,四邊形 ABCD 的頂點都在格點上,如圖所示.則下列結論錯 誤的是( )
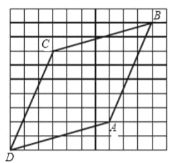
A.![]() B.
B.![]()
C.四邊形![]() 是菱形D.將邊
是菱形D.將邊![]() 向右平移
向右平移![]() 格,再向上平移
格,再向上平移![]() 格就與邊
格就與邊![]() 重合
重合
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠AOB=45°,過OA上到點O的距離分別為1,3,5,7,9,11,的點作OA的垂線與OB相交,得到并標出一組黑色梯形,它們的面積分別為S1,S2,S3,S4,…,觀察圖中的規律,求出第10個黑色梯形的面積S10=_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于平面直角坐標系![]() 中的點
中的點![]() 和
和![]() (半徑為
(半徑為![]() ),給出如下定義:若點
),給出如下定義:若點![]() 關于點
關于點![]() 的對稱點為
的對稱點為![]() ,且
,且![]() ,則稱點
,則稱點![]() 為
為![]() 的稱心點.
的稱心點.
(1)當![]() 的半徑為2時,
的半徑為2時,
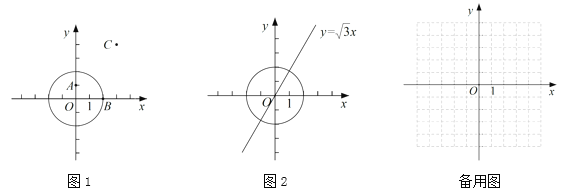
①如圖1,在點![]() ,
,![]() ,
,![]() 中,
中,![]() 的稱心點是 ;
的稱心點是 ;
②如圖2,點![]() 在直線
在直線![]() 上,若點
上,若點![]() 是
是![]() 的稱心點,求點
的稱心點,求點![]() 的橫坐標
的橫坐標![]() 的取值范圍;
的取值范圍;
(2)![]() 的圓心為
的圓心為![]() ,半徑為2,直線
,半徑為2,直線![]() 與
與![]() 軸,
軸,![]() 軸分別交于點
軸分別交于點![]() ,
,![]() .若線段
.若線段![]() 上的所有點都是
上的所有點都是![]() 的稱心點,直接寫出
的稱心點,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了幫助市內一名患“白血病”的中學生,東營市某學校數學社團15名同學積極捐款,捐款情況如下表所示,下列說法正確的是( )
捐款數額 | 10 | 20 | 30 | 50 | 100 |
人數 | 2 | 4 | 5 | 3 | 1 |
A. 眾數是100 B. 中位數是30 C. 極差是20 D. 平均數是30
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com