
【題目】如圖,已知△ABC是等邊三角形,D是AB邊上任意一點,∠CDE=60°,DE與∠ABC外角平分線相交于點E.
(1)求證:CD=DE;

(2)若D是AB延長線上任意一點,∠CDE=60°,DE與∠ABC外角平分線相交于點E.請畫出圖形,判斷CD=DE是否還成立?若成立,請給予證明;若不成立,請說明理由.

【答案】(1)證明見解析;(2)成立,證明見解析.
【解析】
(1)過點D作DF//BC,交AC于F,由等邊三角形的性質可得AF=AD,進而可得CF=BD,根據外角性質可知∠FCD+∠CDF=60°,由∠CDE=60°,∠ADF=60°可得∠CDF+∠EDB=60°,進而可得∠FCD=∠EDB,由BE是外角平分線可得∠CBE=60°,即可證明∠DBE=∠CFD=120°,即可證明△CFD≌△DEB,進而可得CD=DE;(2)過點D作DP//BC,交AC延長線于點P,由等邊三角形及平行線性質可得CP=BD,根據外角性質可得∠PCD=∠A+∠ADC=60°+∠ADC,由∠BDE=∠CDE+∠ADC=60°+∠ADC可證明∠PCD=∠BDE,根據BE是外角平分線可得∠EBD=∠P=60°,即可證明△PCD≌△BDE,進而可得CD=DE.
(1)如圖,過點D作DF//BC,交AC于F,
∵△ABC是等邊三角形,DF//BC,
∴CF=BD,∠AFD=60°,
∴∠CFD=180°-60°=120°,
∵DE是外角平分線,
∴∠CBE=60°,
∴∠DBE=120°,
∴∠CFD=∠DBE,
∵∠FCD+∠CDF=∠AFD=60°,∠BDE+∠CDF=180°-∠ADF-∠CDE=180°-60°-60°=60°,
∴∠FCD=∠BDE,
∴△CFD≌△DEB,
∴CD=DE.

(2)過點D作DP//BC,交AC延長線于點P,
∵△ABC是等邊三角形,DP//BC,
∴PC=BD,∠P=60°,
∵BE是外角平分線,
∴∠DBE=60°,
∴∠DBE=∠P,
∵∠PCD=∠A+∠ADC=60°+∠ADC,∠BDE=∠ADC+∠CDE=60°+∠ADC,
∴∠PCD=∠BDE,
∴△PCD≌△BDE,
∴CD=DE



 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案科目:初中數學 來源: 題型:
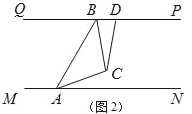
【題目】“一帶一路”讓中國和世界更緊密,“中歐鐵路”為了安全起見在某段鐵路兩旁安置了兩座可旋轉探照燈.如圖1所示,燈A射線從AM開始順時針旋轉至AN便立即回轉,燈B射線從BP開始順時針旋轉至BQ便立即回轉,兩燈不停交叉照射巡視.若燈A轉動的速度是每秒2度,燈B轉動的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若燈B射線先轉動30秒,燈A射線才開始轉動,在燈B射線到達BQ之前,A燈轉動幾秒,兩燈的光束互相平行?
(3)如圖2,若兩燈同時轉動,在燈A射線到達AN之前.若射出的光束交于點C,過C作∠ACD交PQ于點D,且∠ACD=120°,則在轉動過程中,請探究∠BAC與∠BCD的數量關系是否發生變化?若不變,請求出其數量關系;若改變,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,回答有關問題:在實數這章中,遇到過![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 這樣的式子,我們把這樣的式子叫做二次根式,根號下的數叫做被開方數.如果一個二次根式的被開方數中有的因數能開得盡方,可以利用
這樣的式子,我們把這樣的式子叫做二次根式,根號下的數叫做被開方數.如果一個二次根式的被開方數中有的因數能開得盡方,可以利用![]() =
=![]() (a≥0,b≥0);
(a≥0,b≥0);![]() (a≥0,b>0)將這些因數開出來,從而將二次根式化簡.當一個二次根式的被開方數中不含開得盡方的因數或者被開方數中不含有分母時,這樣的二次根式叫做最簡二次根式,例如,
(a≥0,b>0)將這些因數開出來,從而將二次根式化簡.當一個二次根式的被開方數中不含開得盡方的因數或者被開方數中不含有分母時,這樣的二次根式叫做最簡二次根式,例如,![]() 化成最簡二次根式是
化成最簡二次根式是![]() ,
,![]() 化成最簡二次根式是3
化成最簡二次根式是3![]() ,幾個二次根式化成最簡二次根式以后,如果被開方數相同,這幾個二次根式叫做同類二次根式,如上面的例子中的
,幾個二次根式化成最簡二次根式以后,如果被開方數相同,這幾個二次根式叫做同類二次根式,如上面的例子中的![]() 和
和![]() 就是同類二次根式.
就是同類二次根式.
(1)請判斷下列各式中,哪些是同類二次根式?![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)二次根式中的同類二次根式可以像整式中的同類項一樣合并,請計算:![]() +
+![]() -
-![]() -
-![]() +
+![]() -
-![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人以各自的交通工具、相同路線,前往距離單位10km的培訓中心參加學習.圖中l甲、l乙分別表示甲、乙前往目的地所走的路程S(km)隨時間t(分)變化的函數圖象.以下說法:①乙比甲提前12分鐘到達;②乙走了8km后遇到甲;③乙出發6分鐘后追上甲;④甲走了28分鐘時,甲乙相距3km.其中正確的是( )

A. 只有① B. ①③ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
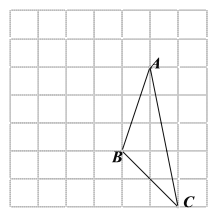
【題目】畫圖(只能借助于網格)并填空:
如圖,每個小正方形的邊長為![]() 個單位,每個小正方形的頂點叫格點.
個單位,每個小正方形的頂點叫格點.
(1)將![]() 向左平移
向左平移![]() 格,再向上平移
格,再向上平移![]() 格,請在圖中畫出平移后的
格,請在圖中畫出平移后的![]() ;
;
(2)![]() 的面積為 ;
的面積為 ;
(3)利用網格在圖中畫出△ABC的中線![]() ,高線
,高線![]() ;
;
(4)在圖中能使![]() 的格點
的格點![]() 的個數有 個(點
的個數有 個(點![]() 異于
異于![]() ).
).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,一次函數的圖象經過點A(2,3)與點B(0,5).
(1)求此一次函數的表達式;
(2)若點P為此一次函數圖象上一點,且△POB的面積為10,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了創建書香校園,今年又購進一批圖書,經了解,科普書的單價比文學書的單價多4元,用1200元購進的科普書與用800元購進的文學書本數相等.
(1)今年購進的文學書和科普書的單價各是多少元?
(2)該校購買這兩種書共180本,總費用不超過2000元,且購買文學書的數量不多于42本,應選擇哪種購買方案可使總費用最低?最低費用是多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com