
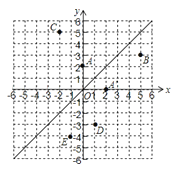
【題目】如圖,在平面直角坐標系中,直線L是第一、三象限的角平分線.
(1)由圖觀察易知A(0,2)關于直線l的對稱點A′的坐標為(2,0),請在圖中分別標明B(5,3)、C(﹣2,5)關于直線l的對稱點B′、C′的位置,并寫出他們的坐標:B′ 、C′ ;
(2)結合圖形觀察以上三組點的坐標,直接寫出坐標面內任一點P(a,b)關于第一、三象限的角平分線l的對稱點P′的坐標為 ;
(3)已知兩點D(1,﹣3)、E(﹣1,﹣4),試在直線L上畫出點Q,使△QDE的周長最小,并求△QDE周長的最小值.
【答案】(1)B'(3,5),C'(5,﹣2);(2)(b,a);(3)![]() 。
。
【解析】分析:(1)根據對稱軸為第一、三象限的角平分線,結合圖形得出B′、C′兩點坐標;(2)由(1)的結論,并與B、C兩點坐標進行比較,得出一般規律;(3)由軸對稱性作出滿足條件的Q點,求出直線D′E的解析式,與直線y=x聯立,可求Q點的坐標,得出結論.
本題解析:
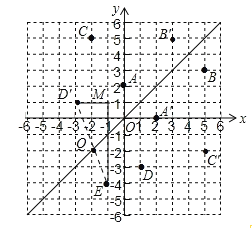
解:(1)如圖,由點關于直線y=x軸對稱可知:B'(3,5),C'(5,﹣2).
(2)由(1)的結果可知,坐標平面內任一點P(a,b)關于第一、三象限的角平分線l的對稱點P′的坐標為 (b,a).
由(2)得,D(1,﹣3)關于直線l的對稱點D'的坐標為(﹣3,1),連接D'E交直線l于點Q,此時點Q到D、E兩點的距離之和最小,
D'E=![]() =
=![]() =
=![]() ,
,
![]() ∴
∴![]() 周長的最小值
周長的最小值![]() .+
.+![]() .
.


科目:初中數學 來源: 題型:
【題目】某汽車制造廠接受了在預定期限內生產一批汽車的任務,如果每天生產35輛,則差10輛才能完成任務;如果每天生產40輛,則可超額生產20輛.試求預定期限是多少天?計劃生產多少輛汽車?
若設預定期限為x天,計劃生產y輛汽車,請你根據題意填空,并列出方程組求x與y的值.
(1)若每天生產35輛,在預定期限x天內可生產__________輛,比計劃產量y輛汽車__________(“多”或“少”)生產10輛,則可得二元一次方程______________________.
(2)若每天生產40輛,在預定期限x天內可生產__________輛,比計劃產量y__________(填“多”或“少”)生產20輛,則可列二元一次方程_________________________.
(3)列方程組_________________________,并解得________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,下列各組角的位置,判斷錯誤的是( ) 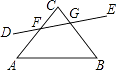
A.∠C和∠CFG是同旁內角
B.∠CGF和∠AFG是內錯角
C.∠BGF和∠A是同旁內角
D.∠BGF和∠AFD是同位角
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解某校300名初三學生的睡眠時間,從中抽取30名學生進行調查,在這個問題中,下列說法正確的是( )
A.300名學生是總體
B.300是樣本容量
C.30名學生是抽取的一個樣本
D.30是樣本的容量
查看答案和解析>>
科目:初中數學 來源: 題型:
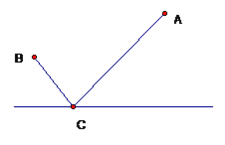
【題目】傳說在古羅馬時代的亞歷山大城有一位精通數學和物理的學者,名叫海倫。一天,一位將軍專程去拜訪他,想他請叫一個百思不得其解的問題。將軍每天都從軍營A出發(如圖),先到河邊C處飲馬,然后再去河岸的同側B開會,他應該怎樣走才能使路程最短? 據說當時海輪略加思索就解決了它。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題為真命題的是
A. 有兩邊及一角對應相等的兩個三角形全等
B. 方程 x2+2x+3=0有兩個不相等的實數根
C. 面積之比為1∶2的兩個相似三角形的周長之比是1∶4
D. 順次連接任意四邊形各邊中點得到的四邊形是平行四邊形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若坐標平面上點P(a,1)與點Q(-4,b)關于x軸對稱,則( )
A. a=4,b=-1 B. a=-4,b=1 C. a=-4,b=-1 D. a=4,b=l
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com