Question

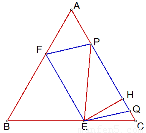
如圖,等邊△ABC的邊長為4,E是邊BC上的動點,EH⊥AC于H,過E作EF∥AC,交線段AB于點F,在線段AC上取點P,使PE＝EB．設EC＝x（0＜x≤2）．

（1）請直接寫出圖中與線段EF相等的兩條線段（不再另外添加輔助線）；

（2）Q是線段AC上的動點,當四邊形EFPQ是平行四邊形時,求平行四邊形EFPQ的面積（用含的代數式表示）；

（3）當（2）中 的平行四邊形EFPQ面積最大值時,以E為圓心,r為半徑作圓,根據⊙E與此時平行四邊形EFPQ四條邊交點的總個數,求相應的r的取值范圍．

 

Answer 1

【答案】

（1）BE、PE；

（2）；

（3）當⊙E與平行四邊形EFPQ的四條邊交點的總個數是2個時,0＜r＜；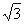

當⊙E與平行四邊形EFPQ的四條邊交點的總個數是4個時,r＝；??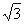

當⊙E與平行四邊形EFPQ的四條邊交點的總個數是6個時,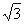＜r＜2；

當⊙E與平行四邊形EFPQ的四條邊交點的總個數是3個時,r＝2；

當⊙E與平行四邊形EFPQ的四條邊交點的總個數是0個時,r＞2．

【解析】

試題分析：（1）根據三角形ABC是等邊三角形和EF∥AC,可得等邊三角形BEF,則可寫出與EF相等的線段；

（2）根據（1）可知EF=BE=4﹣x,要求平行四邊形的面積,只需求得EF邊上的高．作EH⊥AC于H,根據30度的直角三角形EHC進行表示EH的長,進一步求得平行四邊形的面積；

（3）根據二次函數的頂點式或頂點的公式法求得平行四邊形的面積的最大值時x的值,分析平行四邊形的位置和形狀．然后根據公共點的個數分析圓和平行四邊形的各邊的位置關系,進一步根據圓和直線的位置關系求得r的取值范圍．

試題解析：（1）BE、PE、BF三條線段中任選兩條；

（2）作EQ∥FP交FE于E,

設EC為x

∵EH⊥AC,

∴∠EHC=90°

∴△CHE為直角三角形

∵△ABC為等邊三角形,

∴∠C=60°

在Rt△CHE中,∠CHE=90°,∠C=60°,

∠HEC=180°﹣∠C﹣∠EHC=30°

∴2HC=EC

∵HE2=EC2﹣HC2

∴,

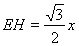∵EF∥AC,FP∥EQ

∴四邊形EFPQ為平行四邊形

∴PQ=FE

又∵PE=BE

∴PQ=EF=BE=4﹣x

∴；

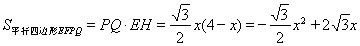（3）因為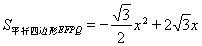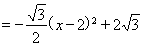,所以當x＝2時,平行四邊形EFPQ的面積最大．此時E、F、P分別為△ABC的三邊BC、AB、AC的中點,且C、Q重合,四邊形EFPQ是邊長為2的菱形（如圖）．

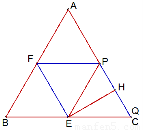
過點E點作ED⊥FP于D,則ED＝EH＝．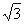

當⊙E與平行四邊形EFPQ的四條邊交點的總個數是2個時,0＜r＜；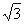

當⊙E與平行四邊形EFPQ的四條邊交點的總個數是4個時,r＝；??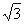

當⊙E與平行四邊形EFPQ的四條邊交點的總個數是6個時,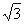＜r＜2；

當⊙E與平行四邊形EFPQ的四條邊交點的總個數是3個時,r＝2；

當⊙E與平行四邊形EFPQ的四條邊交點的總個數是0個時,r＞2．

考點：二次函數綜合題．