
【題目】如圖,∠AOB是平角,∠DOE=90°,OC平分∠DOB.
(1)若∠AOE=32°,求∠BOC的度數;
(2)若OD是∠AOC的角平分線,求∠AOE的度數.

【答案】(1)61°;(2)30°.
【解析】
(1)求出∠AOD和∠BOD,由OC平分∠DOB,求出∠BOC;
(2)根據OC平分∠BOD,OD平分∠AOC得出∠BOC=∠DOC=∠AOD,求出∠AOD即可得出∠AOE.
解:(1)∠AOD=∠DOE﹣∠AOE=90°﹣32°=58°,,
∠BOD=∠AOB﹣∠AOD=180°﹣58°=122°,
又OC平分∠BOD,
所以:∠BOC=![]() ∠BOD=
∠BOD=![]() ×122°=61°;
×122°=61°;
(2)因為OC平分∠BOD,OD平分∠AOC,
所以∠BOC=∠DOC=∠AOD,
又∠BOC+∠DOC+∠AOD=180°,
所以∠AOD=![]() ×180°=60°,
×180°=60°,
所以∠AOE=∠DOE﹣∠AOD=90°﹣60°=30°.


科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,延長AB到點E,使BE=AB,連接DE交BC于點F,則下列結論不一定成立的是( ) 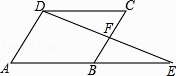
A.∠E=∠CDF
B.EF=DF
C.AD=2BF
D.BE=2CF
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,直線y1=2x﹣2與坐標軸交于A、B兩點,與雙曲線y2= ![]() (x>0)交于點C,過點C作CD⊥x軸,且OA=AD,則以下結論: ①當x>0時,y1隨x的增大而增大,y2隨x的增大而減小;
(x>0)交于點C,過點C作CD⊥x軸,且OA=AD,則以下結論: ①當x>0時,y1隨x的增大而增大,y2隨x的增大而減小;
②k=4;
③當0<x<2時,y1<y2;
④如圖,當x=4時,EF=4.
其中正確結論的個數是( )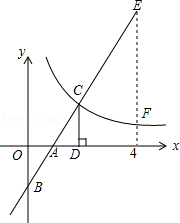
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平移線段AB,使點A移動到點A1.
(1)畫出平移后的線段A1B1,分別連接AA1,BB1.
(2)分別畫出AC⊥A1B1于點C,AD⊥BB1于點D.
(3)AA1與BB1之間的距離,就是線段 的長度.
(4)線段AB平移的距離,就是線段 的長度.
(5)線段BD的長度,是點B到直線 的距離.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一塊長為a米,寬為b米的矩形空地建成一個矩形花園,要求在花園中修兩條入口寬均為x米的小道,其中一條小道兩邊分別經過矩形一組對角頂點,剩余的地方種植花草,現有從左至右三種設計方案如圖所示,種植花草的面積分別為S1,S2和S3,則它們的大小關系為( )

A. S3<S1<S2 B. S1<S2<S3 C. S2<S1<S3 D. S1=S2=S3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線l:y= ![]() x,過點A(0,1)作y軸的垂線交直線l于點B,過點B作直線l的垂線交y軸于點A1;過點A1作y軸的垂線交直線l于點B1 , 過點B1作直線l的垂線交y軸于點A2;…按此作法繼續下去,則點A2015的坐標為( )
x,過點A(0,1)作y軸的垂線交直線l于點B,過點B作直線l的垂線交y軸于點A1;過點A1作y軸的垂線交直線l于點B1 , 過點B1作直線l的垂線交y軸于點A2;…按此作法繼續下去,則點A2015的坐標為( )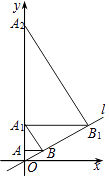
A.(0,42015)
B.(0,42014)
C.(0,32015)
D.(0,32014)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,射線OA的方向是北偏東20°,射線OB的方向是北偏西40°,OD是OB的反向延長線.若OC是∠AOD的平分線,則∠BOC=_____°,射線OC的方向是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C在⊙O上,∠CAB的平分線交⊙O于點D,過點D作AC的垂線交AC的延長線于點E,連接BC交AD于點F. 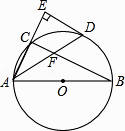
(1)猜想ED與⊙O的位置關系,并證明你的猜想;
(2)若AB=6,AD=5,求AF的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com