
【題目】整頓藥品市場、降低藥品價格是國家的惠民政策之一.根據國家《藥品政府定價辦法》,某省有關部門規定:市場流通藥品的零售價格不得超過進價的15%.根據相關信息解決下列問題:
(1)降價前,甲乙兩種藥品每盒的出廠價格之和為6.6元.經過若干中間環節,甲種藥品每盒的零售價格比出廠價格的5倍少2.2元,乙種藥品每盒的零售價格是出廠價格的6倍,兩種藥品每盒的零售價格之和為33.8元.那么降價前甲、乙兩種藥品每盒的零售價格分別是多少元?
(2)降價后,某藥品經銷商將上述的甲、乙兩種藥品分別以每盒8元和5元的價格銷售給醫院,醫院根據實際情況決定:對甲種藥品每盒加價15%、對乙種藥品每盒加價10%后零售給患者.實際進藥時,這兩種藥品均以每10盒為1箱進行包裝.近期該醫院準備從經銷商處購進甲乙兩種藥品共100箱,其中乙種藥品不少于40箱,銷售這批藥品的總利潤不低于900元.請問購進時有哪幾種搭配方案?
【答案】(1)降價前甲、乙兩種藥品每盒的零售價格分別是15.8元和18元;(2)有3種方案供選擇:第一種方案,甲藥品購買58箱,乙藥品購買42箱;第二種方案,甲藥品購買59箱,乙藥品購買41箱;第三種方案,甲藥品購買60箱,乙藥品購買40箱.
【解析】分析:(1)、首先設甲種藥品的出廠價格為每盒x元,乙種藥品的出廠價格為每盒y元,根據題意列出方程組,從而得出x和y的值,然后求出零售價;(2)、設購進甲藥品z箱(z為非負整數),購進乙藥品(100﹣z)箱,根據題意列出不等式組,從而得出不等式組的解,根據解為整數得出不同的情況.
詳解:(1)設甲種藥品的出廠價格為每盒x元,乙種藥品的出廠價格為每盒y元.
則根據題意列方程組得:![]() ,
,
解之得:![]() ,
,
∴5×3.6﹣2.2=18﹣2.2=15.8(元), 6×3=18(元),
答:降價前甲、乙兩種藥品每盒的零售價格分別是15.8元和18元;
(2)設購進甲藥品z箱(z為非負整數),購進乙藥品(100﹣z)箱.
則根據題意列不等式組得:![]() ,
,
解得:57![]() ≤z≤60,
≤z≤60,
則z可取:58,59,60,此時100﹣z的值分別是:42,41,40;
有3種方案供選擇:第一種方案,甲藥品購買58箱,乙藥品購買42箱;
第二種方案,甲藥品購買59箱,乙藥品購買41箱;
第三種方案,甲藥品購買60箱,乙藥品購買40箱.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖1,O為直線AB上一點,OC為射線,∠AOC=40°,將一個三角板的直角頂點放在點O處,一邊OD在射線OA上,另一邊OE與OC都在直線AB的上方.
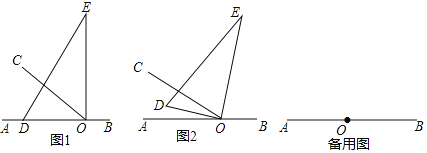
(1)將三角板繞點O順時針旋轉,若OD恰好平分∠AOC(如圖2),試說明OE平分∠BOC;
(2)將三角板繞點O在直線AB上方順時針旋轉,當OD落在∠BOC內部,且∠COD=![]() ∠BOE時,求∠AOE的度數:
∠BOE時,求∠AOE的度數:
(3)將圖1中的三角板和射線OC同時繞點O,分別以每秒6°和每秒2°的速度順時針旋轉一周,求第幾秒時,OD恰好與OC在同一條直線上?
查看答案和解析>>
科目:初中數學 來源: 題型:
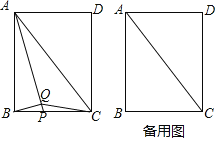
【題目】如圖,在矩形![]() 中,
中,![]() 為對角線,點
為對角線,點![]() 為
為![]() 邊上一動點,連結
邊上一動點,連結![]() ,過點
,過點![]() 作
作![]() ,垂足為
,垂足為![]() ,連結
,連結![]() .
.
(1)證明:![]() ;
;
(2)當點![]() 為
為![]() 的中點時,若
的中點時,若![]() ,求
,求![]() 的度數;
的度數;
(3)當點![]() 運動到與點
運動到與點![]() 重合時,延長
重合時,延長![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,則
,則![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法錯誤的有( )個
①互為相反數的數的立方根也互為相反數;
②![]() 不是整式;
不是整式;
③算術平方根等于它本身的數只有零;
④實數和數軸上的點一一對應;
⑤任何兩數相加,和不小于任何一個加數.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖 ,已知△ ABC 中,點 D 、E 是 BC 邊上兩點,且 ADAE ,BAECAD 90 ,
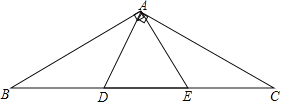
(1)試說明△ABE 與△ACD 全等的理由;
(2)如果 ADBD ,試判斷△ADE 的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,在
,在![]() 中,
中,![]() ,過點
,過點![]() 的直線
的直線![]() ,
,![]() 為
為![]() 邊上一點,過點
邊上一點,過點![]() 作
作![]() ,交直線
,交直線![]() 于點
于點![]() ,垂足為點
,垂足為點![]() ,連接
,連接![]() .
.
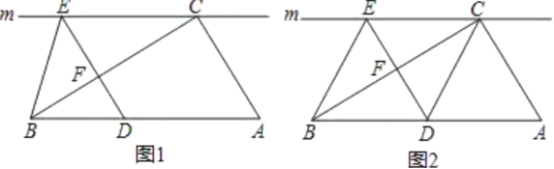
(1)求證:![]() ;
;
(2)如圖![]() ,當點
,當點![]() 是
是![]() 中點時,連接
中點時,連接![]() .
.
①四邊形![]() 是什么特殊四邊形?說明你的理由;
是什么特殊四邊形?說明你的理由;
②當![]()
![]() 時,四邊形
時,四邊形![]() 是正方形.(直接寫出答案)
是正方形.(直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次數學活動中,小輝將一塊矩形紙片![]() 對折,使
對折,使![]() 與
與![]() 重合,得到折痕
重合,得到折痕![]() ,把紙片展開,再一次折疊紙片,使點
,把紙片展開,再一次折疊紙片,使點![]() 落在
落在![]() 上,并使折痕經過點
上,并使折痕經過點![]() ,得到折痕
,得到折痕![]() .同時,得到了線段
.同時,得到了線段![]() .
.
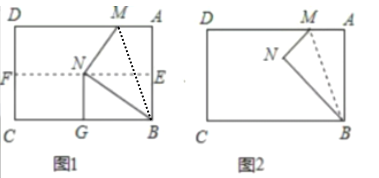
(1)如圖![]() ,若點
,若點![]() 剛好落在折痕
剛好落在折痕![]() 上時,
上時,
①過![]() 作
作![]() ,求證:
,求證:![]() ;
;
②求![]() 的度數;
的度數;
(2)如圖![]() ,當
,當![]() 為射線
為射線![]() 上的一個動點時,已知
上的一個動點時,已知![]() ,
,![]() ,若
,若![]() 的直角三角形時,請直接寫出
的直角三角形時,請直接寫出![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點M,N把線段AB分割成AM,MN和BN,若以AM,MN,BN為邊的三角形是一個直角三角形,則稱點M,N是線段AB的勾股分割點
(1)已知點M,N是線段AB的勾股分割點,若AM=3,MN=4,則BN的長為__________;
(2)已知點C是線段AB上的一定點,其位置如圖2所示,請在BC上畫一點D,使C,D是線段AB的勾股分割點(要求尺規作圖,不寫畫法,保留作圖痕跡,畫出一種情形即可)
![]()

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB=AD,∠C=90°,以AB為直徑的⊙O交AD于點E,CD=ED,連接BD交⊙O于點F.
(1)求證:BC與⊙O相切;
(2)若BD=10,AB=13,求AE的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com