
【題目】王華、張偉兩位同學分別將自己10次數學自我檢測的成績繪制成如下統計圖:
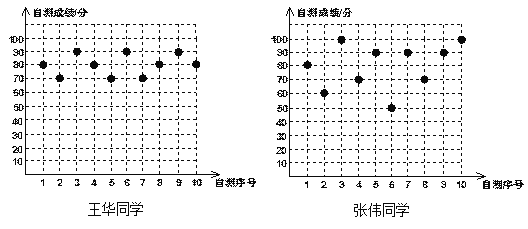
(1)根據上圖中提供的數據列出如下統計表:
平均成績(分) | 中位數(分) | 眾數(分) | 方差(S2) | |
王華 | 80 | b | 80 | d |
張偉 | a | 85 | c | 260 |
則a= ,b= ,c= ,d= ,
(2)將90分以上(含90分)的成績視為優秀,則優秀率高的是 .
(3)現在要從這兩個同學選一位去參加數學競賽,你可以根據以上的數據給老師哪些建議?
【答案】(1)80,80,90,60;(2)張偉;(3)答案見解析
【解析】(1)由平均數、方差的公式計算平均成績即可;將王華的成績按大小順序排列,中間兩個數的平均數,即為中位數;一組數據中出現次數最多的一個數即為眾數;
(2)比較哪位同學的成績在90分以上(含90分)的成績多,即優秀率高;
(3)不同分析角度,得到的結果不同,只要建議合理就行,如:比較這兩位同學的方差,方差越小,成績越穩定.
解:(1)∵![]() 張偉 =(80+60+100+70+90+50+90+70+90+100)÷10=80,
張偉 =(80+60+100+70+90+50+90+70+90+100)÷10=80,
∴![]()
∵S 王華 2 =60,
∴![]()
∵張偉的成績中90分出現的次數最多,則張偉的成績的眾數為90;
∴![]()
故答案為: a=80 ,b=80,c=90,d=60 ,
(2)張偉成績的優秀率=50%,王華成績的優秀率=30%,
∴優秀率高的同學是張偉;
故答案為:張偉.
(3)∵S 王華2 <S 張偉2 ,
∴選王華去參加數學競賽.(根據以上數據提供的建議合理即可)


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:初中數學 來源: 題型:
【題目】(12分)如圖,在△ABC中,AB=AC,以AB為直徑的⊙O分別交BC,AC于點D,E,DG⊥AC于點G,交AB的延長線于點F.
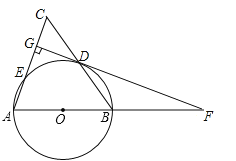
(1)求證:直線FG是⊙O的切線;
(2)若AC=10,cosA=![]() ,求CG的長.
,求CG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
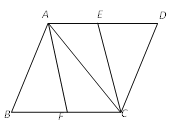
【題目】如圖,在□ABCD中,E、F分別是AD、BC的中點,連接AC、CE、AF.
(1)求證△ABF ≌ △CDE;
(2)若AB=AC,求證四邊形AFCE是矩形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠A=60°,BD,CD分別平分∠ABC,∠ACB,M,N,Q分別在DB,DC,BC的延長線上,BE,CE分別平分∠MBC,∠BCN,BF,CF分別平分∠EBC,∠ECQ,則∠F= . 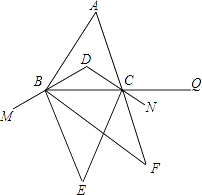
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面的材料:
如圖①,在![]() 中,試說明
中,試說明![]() .
.
分析:通過畫平行線,將![]() 、
、![]() 、
、![]() 作等量代換,使各角之和恰為一個平角,依輔助線不同而得多種方法.
作等量代換,使各角之和恰為一個平角,依輔助線不同而得多種方法.
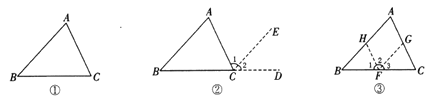
解:如圖②,延長![]() 到點
到點![]() ,過點
,過點![]() 作
作![]() //
//![]() .
.
因為![]() //
//![]() (作圖所知),
(作圖所知),
所以![]() ,
,![]() (兩直線平行,同位角、內錯角相等).
(兩直線平行,同位角、內錯角相等).
又因為![]() (平角的定義),
(平角的定義),
所以![]() (等量代換).
(等量代換).
如圖③,過![]() 上任一點
上任一點![]() ,作
,作![]() //
//![]() ,
, ![]() //
//![]() ,這種添加輔助線的方法能說
,這種添加輔助線的方法能說![]() 嗎?并說明理由.
嗎?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
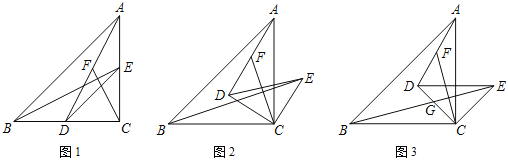
【題目】如圖1,在Rt△ABC中,∠ACB=90°,AC=BC,D,E分別為AC,BC上的點,且CE=CD,連接DE,AD,BE,F為線段AD的中點,連接CF.
(1)求證:BE=2CF;
(2)如圖2,把△DEC繞點C順時針旋轉α角(0°<α<90°),其他條件不變,試探究線段BE與CF的位置關系,并說明理由;
(3)如圖3,把△DEC繞點C順時針旋轉45°,BE,CD交于點G.若∠DCF=30°,求![]() 及
及![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com