
【題目】如圖,△ABC內接于⊙O,且AB為⊙O的直徑.∠ACB的平分線交⊙O于點D,過點D作⊙O的切線PD交CA的延長線于點P,過點A作AE⊥CD于點E,過點B作BF⊥CD于點F.
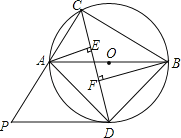
(1)求證:DP∥AB;
(2)若AC=6,BC=8,求線段PD的長.
【答案】解:(1)證明:如圖,連接OD,
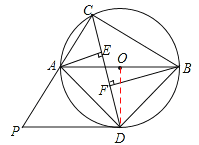
∵AB為⊙O的直徑,∴∠ACB=90°。
∵∠ACB的平分線交⊙O于點D,∴∠ACD=∠BCD=45°。
∴∠DAB=∠ABD=45°。∴△DAB為等腰直角三角形。
∴DO⊥AB。
∵PD為⊙O的切線,∴OD⊥PD。
∴DP∥AB。
(2)在Rt△ACB中,![]() ,
,
∵△DAB為等腰直角三角形,∴![]() 。
。
∵AE⊥CD,∴△ACE為等腰直角三角形。∴![]() 。
。
在Rt△AED中,![]() ,
,
∴![]() 。
。
∵AB∥PD,∴∠PDA=∠DAB=45°。∴∠PAD=∠PCD。
又∵∠DPA=∠CPD,∴△PDA∽△PCD。∴![]() 。
。
∴PA=![]() PD,PC=
PD,PC=![]() PD。
PD。
又∵PC=PA+AC,∴![]() PD+6=
PD+6=![]() PD,解得PD=
PD,解得PD=![]() 。
。
【解析】
試題分析:(1)連接OD,由AB為⊙O的直徑,根據圓周角定理得∠ACB=90°,再由∠ACD=∠BCD=45°,則∠DAB=∠ABD=45°,所以△DAB為等腰直角三角形,所以DO⊥AB,根據切線的性質得OD⊥PD,于是可得到DP∥AB。
(2)先根據勾股定理計算出AB=10,由于△DAB為等腰直角三角形,可得到![]() ;由△ACE為等腰直角三角形,得到
;由△ACE為等腰直角三角形,得到![]() ,在Rt△AED中利用勾股定理計算出DE=
,在Rt△AED中利用勾股定理計算出DE=![]() ,則CD=
,則CD=![]() ,易證得∴△PDA∽△PCD,得到
,易證得∴△PDA∽△PCD,得到![]() ,所以PA=
,所以PA=![]() PD,PC=
PD,PC=![]() PD,然后利用PC=PA+AC可計算出PD。
PD,然后利用PC=PA+AC可計算出PD。


科目:初中數學 來源: 題型:
【題目】小明在上學的路上(假定從家到校只有這一條路)發現忘帶眼鏡,立刻停下,往家里打電話,媽媽接到電話后立刻帶上眼鏡趕往學校.同時,小明原路返回,兩人相遇后小明立即趕往學校,媽媽回家,媽媽要15分鐘到家,小明再經過3分鐘到校.小明始終以100米/分的速度步行,小明和媽媽之間的距離y(米)與小明打完電話后的步行時間t(分)之間函數圖象如圖所示,則下列結論:①打電話時,小明與媽媽的距離為1250米;②打完電話后,經過23分鐘小明到達學校;③小明與媽媽相遇后,媽媽回家的速度為150米/分;④小明家與學校的距離為2550米.其中正確的有 .(把正確的序號都填上)
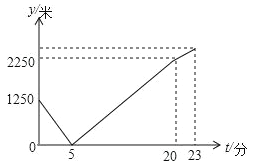
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知矩形ABCD(AB<AD).
(1)請用直尺和圓規按下列步驟作圖,保留作圖痕跡;
①以點A為圓心,以AD的長為半徑畫弧交邊BC于點E,連接AE;
②作∠DAE的平分線交CD于點F;
③連接EF;
(2)在(1)作出的圖形中,若AB=8,AD=10,則tan∠FEC的值為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀并解決問題.
對于形如![]() 這樣的二次三項式,可以用公式法將它分解成
這樣的二次三項式,可以用公式法將它分解成 ![]() 的形式.但對于二次三項式
的形式.但對于二次三項式![]() ,就不能直接運用公式了.此時,我們可以在二次三項式
,就不能直接運用公式了.此時,我們可以在二次三項式![]() 中先加上一項
中先加上一項 ![]() ,使它與
,使它與![]() 的和成為一個完全平方式,再減去
的和成為一個完全平方式,再減去![]() ,整個式子的值不變,于是有:
,整個式子的值不變,于是有:
![]()
像這樣,先添﹣適當項,使式中出現完全平方式,再減去這個項,使整個式子的值不變的方法稱為“配方法”.
(1)利用“配方法”分解因式:![]() .
.
(2)若 a b 5 , ab 6 ,求:①![]() ;②
;② ![]() 的值.
的值.
(3)已知 x 是實數,試比較![]() 與
與![]() 的大小,說明理由.
的大小,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從甲地到乙地有兩條公路,一條是全長600km的普通公路,另一條是全長480km的高速公路,某客車在高速公路上行駛的平均速度比在普通公路上快45![]() /
/![]() ,由高速公路從甲地到乙地所需的時間是由普通公路從甲地到乙地所需時間的一半,求該客車由高速公路從甲地到乙地所需的時間.
,由高速公路從甲地到乙地所需的時間是由普通公路從甲地到乙地所需時間的一半,求該客車由高速公路從甲地到乙地所需的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,![]() ,點E在邊BC上,
,點E在邊BC上,![]() ,將
,將![]() 沿DE對折至
沿DE對折至![]() ,延長EF交邊AB于點C,連接DG,BF,給出以下結論:
,延長EF交邊AB于點C,連接DG,BF,給出以下結論:![]() ≌
≌![]() ;
;![]() ;
;![]() ;
;![]() ∽
∽![]() ,其中所有正確結論的個數是
,其中所有正確結論的個數是![]()
![]()
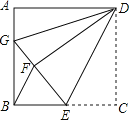
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場購進甲、乙兩種商品,甲種商品共用了2000元,乙種商品共用了2400元![]() 已知乙種商品每件進價比甲種商品每件進價多8元,且購進的甲、乙兩種商品件數相同.
已知乙種商品每件進價比甲種商品每件進價多8元,且購進的甲、乙兩種商品件數相同.
![]() 求甲、乙兩種商品的每件進價;
求甲、乙兩種商品的每件進價;
![]() 該商場將購進的甲、乙兩種商品進行銷售,甲種商品的銷售單價為60元,乙種商品的銷售單價為88元,銷售過程中發現甲種商品銷量不好,商場決定:甲種商品銷售一定數量后,將剩余的甲種商品按原銷售單價的七折銷售;乙種商品銷售單價保持不變
該商場將購進的甲、乙兩種商品進行銷售,甲種商品的銷售單價為60元,乙種商品的銷售單價為88元,銷售過程中發現甲種商品銷量不好,商場決定:甲種商品銷售一定數量后,將剩余的甲種商品按原銷售單價的七折銷售;乙種商品銷售單價保持不變![]() 要使兩種商品全部售完后共獲利不少于2460元,問甲種商品按原銷售單價至少銷售多少件?
要使兩種商品全部售完后共獲利不少于2460元,問甲種商品按原銷售單價至少銷售多少件?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】手機給學生帶來方便的同時也帶來了很大的影響.新化縣某校初一年級在一次家長會上對若干家長進行了一次對“學生使用手機”現象看法的調查,將調查數據整理得如下統計圖(![]() :絕對弊大于利,
:絕對弊大于利,![]() :絕對利大于弊,
:絕對利大于弊,![]() :相對弊大于利,
:相對弊大于利,![]() :相對利大于弊):
:相對利大于弊):
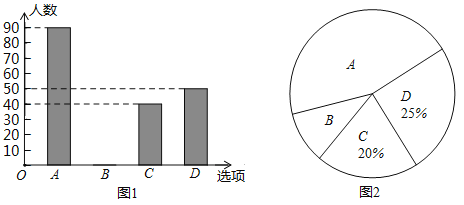
(1)這次調查的家長總人數為多少人?
(2)本次調查的家長中表示“![]() 絕對利大于弊”所占的百分比是多少?并補全條形統計圖.
絕對利大于弊”所占的百分比是多少?并補全條形統計圖.
(3)求扇形統計圖圖2中表示“![]() :絕對弊大于利”的扇形的圓心角度數.
:絕對弊大于利”的扇形的圓心角度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次中學生田徑運動會上,根據參加男子跳高初賽的運動員的成績(單位:m),繪制出如下的統計圖①和圖②,請根據相關信息,解答下列問題:

(Ⅰ)圖1中a的值為 ;
(Ⅱ)求統計的這組初賽成績數據的平均數、眾數和中位數;
(Ⅲ)根據這組初賽成績,由高到低確定9人進入復賽,請直接寫出初賽成績為1.65m的運動員能否進入復賽.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com